I – Définitions et vocabulaire
Exemples :
Pour un vélo, la pression plus ou moins forte sur la manette du frein, on freine plus ou moins rapidement et la distance de freinage est plus ou moins longue. On peut dire que la distance de freinage ![]() est fonction de la pression sur le frein
est fonction de la pression sur le frein ![]()
La table de multiplication par 2 est une fonction : à chaque nombre ![]() , elle associe le nombre
, elle associe le nombre ![]() . On écrit que
. On écrit que ![]() .
.
Un thermomètre est une fonction : à une température donnée, il associe une hauteur de liquide coloré.
Remarques sur le domaine de définition :
Comme cela est dit dans la définition d’une fonction, une fonction peut être définie que pour quelques nombres, pour un intervalle de nombres ou pour l’ensemble des nombres réels.
Exemples :
- Les tables de multiplications apprises à l’école primaire ont comme domaine de définition :
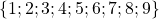 .
. - Un thermomètre usuel en France indique correctement des températures allant de
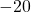 °C à
°C à 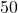 °C. Son domaine de définition exprimé en degrés Celsius est
°C. Son domaine de définition exprimé en degrés Celsius est ![Rendered by QuickLaTeX.com [-20 ; 50]](http://www.rozenblum.com/wp-content/ql-cache/quicklatex.com-7f16a9882b338a216cea577d0ff88244_l3.png) .
. - La fonction, qui à un nombre quelconque
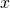 , associe son carré
, associe son carré 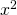 a comme domaine de définition l’ensemble des nombres réels. On dit qu’elle est défini sur
a comme domaine de définition l’ensemble des nombres réels. On dit qu’elle est défini sur 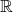 .
.
Remarque sur l’image d’un nombre par une fonction :
Comme cela est dit dans la définition d’une fonction, l’image d’un nombre par une fonction est UNIQUE. Une fonction ne peut pas transformer un nombre ![]() en deux images, car dans ce cas, on ne saurait jamais, laquelle des deux choisir.
en deux images, car dans ce cas, on ne saurait jamais, laquelle des deux choisir.
Pour chaque ![]() , il y a un seul
, il y a un seul ![]() .
.
On peut faire l’analogie avec un miroir. Si vous vous regardez dedans, il vous revoie qu’une seule image de vous.
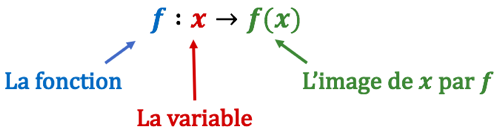
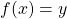
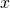 a pour image
a pour image 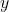
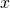 est l’antécédent de
est l’antécédent de 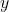
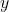 est l’image de
est l’image de 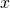
II – Comment définir une fonction ?
1) Par une expression algébrique :
Exemple : ![]()
2) Par un algorithme :
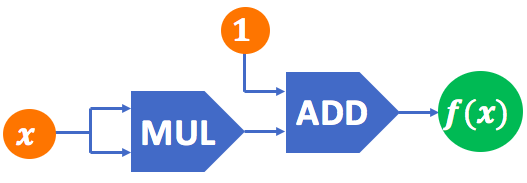 La même fonction
La même fonction ![]() définie par programme de calcul :
définie par programme de calcul :
- choisir un nombre,
- le multiplier par lui-même,
- ajouter 1 au résultat.
3) Par une représentation graphique (définition éventuellement partielle) :
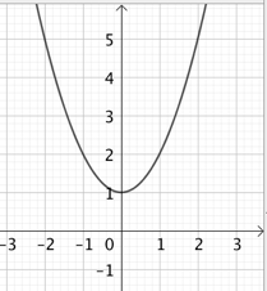 Cette définition est partielle car elle ne permet pas de donner toutes les images lorsque le domaine de définition est grand.
Cette définition est partielle car elle ne permet pas de donner toutes les images lorsque le domaine de définition est grand.
Exemple : la même fonction ![]() est représentée graphiquement. Son domaine de définition est
est représentée graphiquement. Son domaine de définition est ![]() mais la représentation graphique ci-contre est limité à l’intervalle
mais la représentation graphique ci-contre est limité à l’intervalle ![]() .
.
Par contre, la représentation graphique d’une fonction offre de nombreux avantages (voir ci-dessous).
4) Par un tableau de valeurs (définition partielle) :
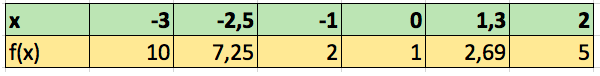 Toujours pour la même fonction.
Toujours pour la même fonction.
Cette définition est partielle car elle ne donne l’image par ![]() que pour quelques valeurs de la variable
que pour quelques valeurs de la variable ![]() . Elle est néanmoins souvent utilisé par décrire le résultat d’une expérience en physique, en chimie, par exemple.
. Elle est néanmoins souvent utilisé par décrire le résultat d’une expérience en physique, en chimie, par exemple.
III – Courbe représentative d’une fonction
L’équation ![]() est appelée équation de la courbe représentative de la fonction
est appelée équation de la courbe représentative de la fonction ![]() .
.
 Soit une fonction définie par son expression algébrique
Soit une fonction définie par son expression algébrique Pour savoir si un point ![]() appartient à la courbe de
appartient à la courbe de ![]() , on calcule
, on calcule ![]() que l’on compare à
que l’on compare à ![]() . Si
. Si ![]() alors
alors ![]() est sur la courbe.
est sur la courbe.
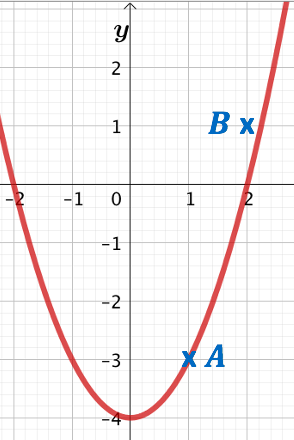 Exemple : Étant donnée la fonction
Exemple : Étant donnée la fonction ![]() , Les points
, Les points ![]() et
et ![]() appartiennent-ils à la courbe représentative de
appartiennent-ils à la courbe représentative de ![]() ?
?
En plaçant ces deux points dans la figure, il semble que la réponse soit positive pour A et négative pour B. On va le vérifier par le calcul :
L’abscisse de ![]() est
est ![]() et son ordonnée est
et son ordonnée est ![]() . Le point
. Le point ![]() appartiendrait à la courbe représentative de
appartiendrait à la courbe représentative de ![]() si
si ![]() .
. ![]() . Donc A est sur la courbe.
. Donc A est sur la courbe.
L’abscisse de ![]() est
est ![]() et son ordonnée est
et son ordonnée est ![]() . Le point
. Le point ![]() appartiendrait à la courbe représentative de
appartiendrait à la courbe représentative de ![]() si
si ![]() .
. ![]() . Donc B n’est pas sur la courbe.
. Donc B n’est pas sur la courbe.
IV – Recherche d’antécédent(s) d’un réel par une fonction
Méthode n°1 : Résolution algébrique de 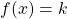
Soit une fonction définie par son expression algébrique ![]() sur un ensemble
sur un ensemble ![]() et un réel
et un réel ![]() . Chercher algébriquement le ou les antécédents de
. Chercher algébriquement le ou les antécédents de ![]() par
par ![]() c’est trouver le ou les valeurs
c’est trouver le ou les valeurs ![]() appartenant à
appartenant à ![]() telles que
telles que ![]() . Cela équivaut à résoudre par le calcul l’équation
. Cela équivaut à résoudre par le calcul l’équation ![]() .
.
 Exemple : Soit une fonction
Exemple : Soit une fonction ![]() . Pour trouver les antécédents, s’ils existent, de
. Pour trouver les antécédents, s’ils existent, de ![]() .Il faut résoudre l’équation :
.Il faut résoudre l’équation : ![]() .
.
![]()
Cette équation a deux solutions : ![]() . Donc les antécédents de
. Donc les antécédents de ![]() par la fonction
par la fonction ![]() sont
sont ![]() et
et ![]() . C’est-à-dire que
. C’est-à-dire que ![]()
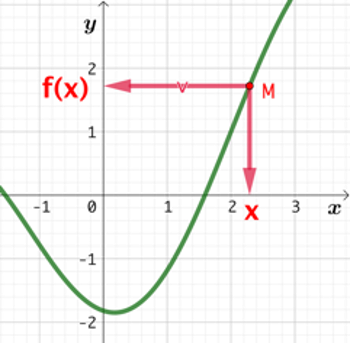
Le nombre ![]() possède-t-il un antécédent par cette même fonction
possède-t-il un antécédent par cette même fonction ![]() ? Tentons de déterminer les solutions de l’équation
? Tentons de déterminer les solutions de l’équation ![]() .
.
![]()
Il est évident que cette équation n’a pas de solution car un carré ne peut être égal à un nombre négatif. Par conséquent ![]() n’a pas d’antécédent par
n’a pas d’antécédent par ![]() .
.
Remarque : L’observation de la courbe représentative de ![]() (figure de droite), nous permet de confirmer ces calculs.
(figure de droite), nous permet de confirmer ces calculs.
Méthode n°2 : Résolution graphique de 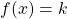 .
.
Soit une fonction définie par son expression algébrique ![]() sur un ensemble
sur un ensemble ![]() et un réel
et un réel ![]() . Chercher graphiquement le ou les antécédents de
. Chercher graphiquement le ou les antécédents de ![]() par
par ![]() c’est résoudre graphiquement l’équation
c’est résoudre graphiquement l’équation ![]() .
.
 Pour cela on trace la droite parallèle à l’axe des abscisses, formée de tous les points d’ordonnées
Pour cela on trace la droite parallèle à l’axe des abscisses, formée de tous les points d’ordonnées ![]() . Puis on cherche les points d’intersection de cette droite avec la courbe représentative de
. Puis on cherche les points d’intersection de cette droite avec la courbe représentative de ![]() . Les abscisses de ces points sont les solutions recherchées. En général, on obtient des valeurs approchées avec une marge d’erreur qui dépend de l’unité choisie pour le repère orthonormé.
. Les abscisses de ces points sont les solutions recherchées. En général, on obtient des valeurs approchées avec une marge d’erreur qui dépend de l’unité choisie pour le repère orthonormé.
Exemple : Pour la fonction dont la courbe est représentée à droite, le nombre ![]() possède trois antécédents dont les valeurs approchées sont :
possède trois antécédents dont les valeurs approchées sont : ![]() .
.
ATTENTION : Il faut toujours vérifier que les solutions trouvées appartiennent bien au domaine de définition ![]() de la fonction
de la fonction ![]() .
.
V – Résolution graphique d’équations
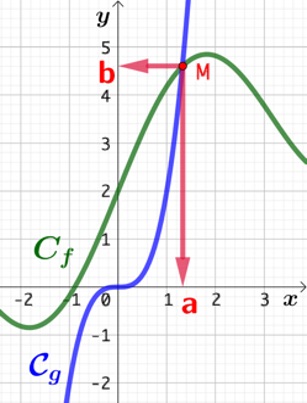 Soient deux fonctions
Soient deux fonctions ![]() et
et ![]() définies un ensemble
définies un ensemble ![]() dont les courbes représentatives sont
dont les courbes représentatives sont ![]() et
et ![]() . Résoudre l’équation
. Résoudre l’équation ![]() consiste à trouver les points d’intersection de
consiste à trouver les points d’intersection de ![]() et
et ![]() .
.
Deux cas possibles :
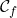 et
et 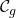 n’ont pas de points d’intersection, alors l’équation
n’ont pas de points d’intersection, alors l’équation 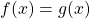 n’a pas de solution.
n’a pas de solution.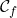 et
et 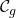 ont des points d’intersection, les solutions de
ont des points d’intersection, les solutions de 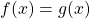 sont les abscisses de ces points.
sont les abscisses de ces points.
Exemple :
Étant données deux fonctions :
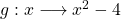 et
et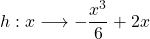 ,
,
on veut résoudre l’équation ![]()
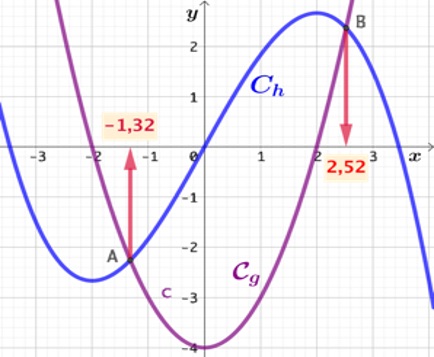 La résolution algébrique est bien trop compliquée (niveau universitaire). On va se contenter d’une résolution graphique.
La résolution algébrique est bien trop compliquée (niveau universitaire). On va se contenter d’une résolution graphique.
On trace les représentations graphiques de ces deux fonctions et on repère les points d’intersection ![]() et
et ![]() .
.
Les valeurs approchées de leurs abscisses respectives, sont les deux solutions réelles de cette équation, soit ![]() et
et ![]() .
.
