Dans ce chapitre on considère une fonction ![]() définie sur un intervalle
définie sur un intervalle ![]() qui peut être l’ensemble des réels
qui peut être l’ensemble des réels ![]() .
.
I – Extremum d’une fonction
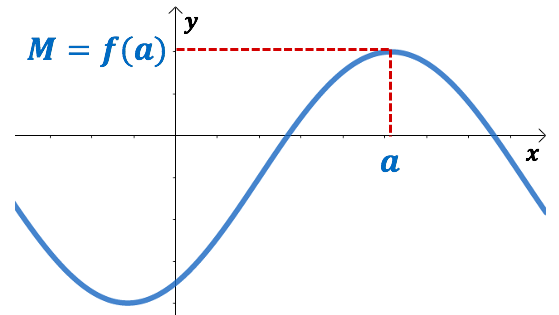
Soit
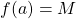 et
et- pour tout
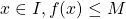
On dit que le maximum ![]() de la fonction
de la fonction ![]() est atteint pour
est atteint pour ![]() .
.
On observe que sur l’intervalle ![]() , la courbe représentative de la fonction
, la courbe représentative de la fonction ![]() présente un sommet.
présente un sommet.
 Soit
Soit 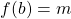 et
et- pour tout
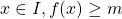
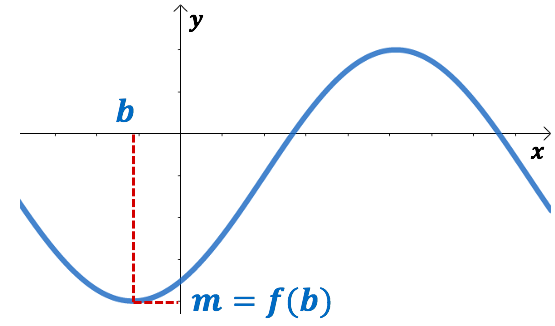
On dit que le minimum ![]() de la fonction
de la fonction ![]() est atteint pour
est atteint pour ![]() .
.
On observe que sur l’intervalle ![]() , la courbe représentative de la fonction
, la courbe représentative de la fonction ![]() présente un creux.
présente un creux.
Vocabulaire : Le minimum et le maximum d’une fonction sont les extrema de cette fonction.
II – Sens de variation d’une fonction
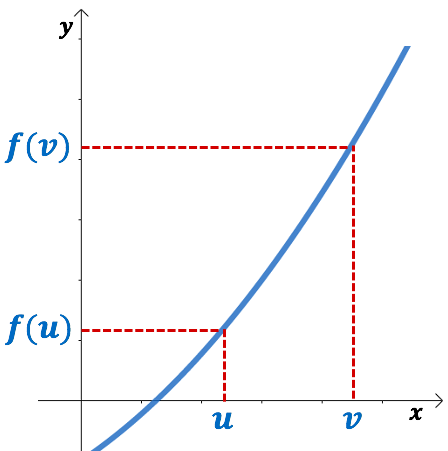
De manière imagée, on observe que sur l’intervalle ![]() , la courbe représentative de la fonction
, la courbe représentative de la fonction ![]() ne cesse de monter.
ne cesse de monter.
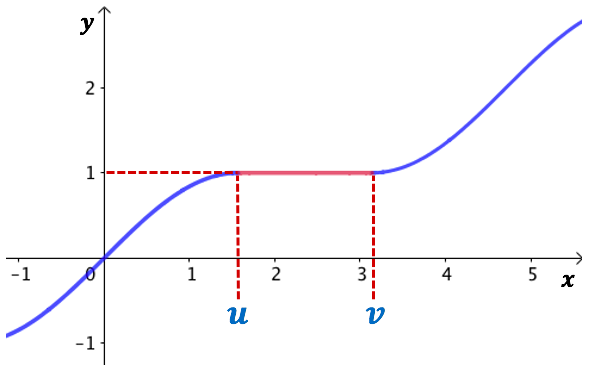
De manière imagée, à la différence d’une fonction strictement croissance, on observe que sur l’intervalle ![]() , la courbe représentative de
, la courbe représentative de ![]() marque une pause dans sa montée. Elle présente au moins un plateau.
marque une pause dans sa montée. Elle présente au moins un plateau.
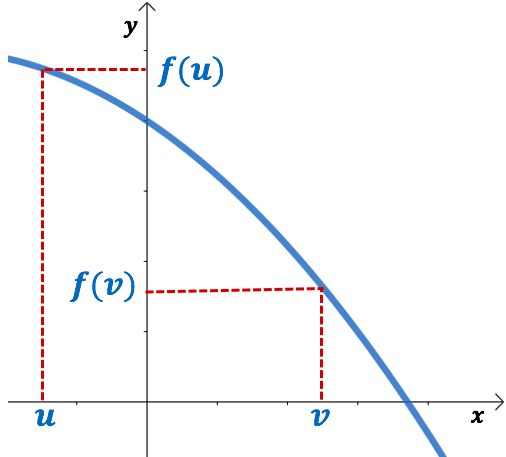
De manière imagée, on observe que sur l’intervalle ![]() , la courbe représentative de la fonction
, la courbe représentative de la fonction ![]() ne cesse de descendre.
ne cesse de descendre.
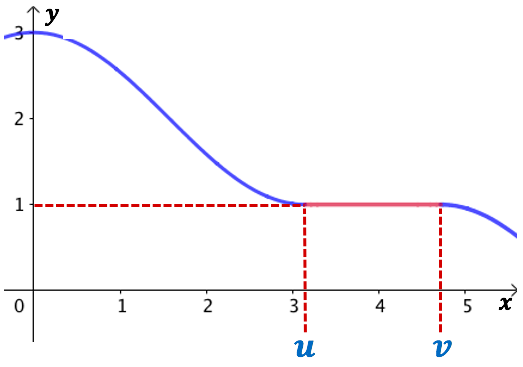
De manière imagée, à la différence d’une fonction strictement décroissance, on observe que sur l’intervalle ![]() , la courbe représentative de
, la courbe représentative de ![]() marque une pause dans sa descente. Elle présente au moins un plateau.
marque une pause dans sa descente. Elle présente au moins un plateau.
Vocabulaire : une fonction croissante ou décroissante sur un intervalle est dite monotone.
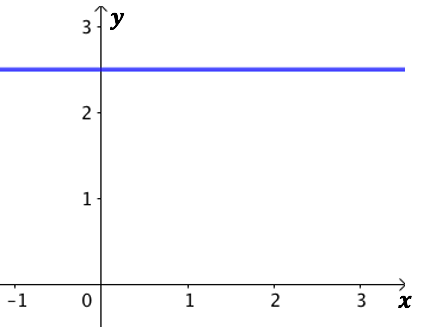 Exemple :
Exemple : ![]() sur
sur ![]() .
.
La courbe représentative de la fonction est une droite parallèle à l’axe des abscisses.
III – Tableau de variation d’une fonction
- les valeurs clés de l’ensemble de définition ;
- les variations de la fonction : Une flèche descendante si la fonction est décroissante, une flèche montante si elle est croissante ;
- Les extrema pour chaque intervalle.
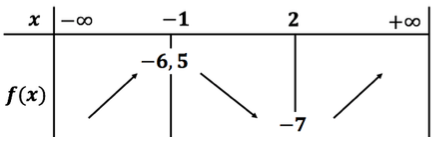 Exemple : le tableau de variation de la fonction
Exemple : le tableau de variation de la fonction ![]() .
.
Que nous apprend ce tableau de variations sur la fonction ![]() ?
?
- La première ligne
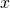 : l’ensemble de définition est
: l’ensemble de définition est 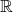
- La deuxième ligne
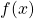 :
:
 possède un maximum
possède un maximum 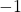 qui est atteint en
qui est atteint en 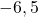
 possède un minimum
possède un minimum 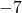 qui est atteint en
qui est atteint en 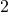
 est croissante sur
est croissante sur ![Rendered by QuickLaTeX.com ]-\infty ; -1[](http://www.rozenblum.com/wp-content/ql-cache/quicklatex.com-fa2b3de249cc68c45cedcd9b67df8744_l3.png) et
et ![Rendered by QuickLaTeX.com ]2 ; +\infty[](http://www.rozenblum.com/wp-content/ql-cache/quicklatex.com-cade1594e9ec79800623f1c436492c45_l3.png)
 est décroissante sur
est décroissante sur ![Rendered by QuickLaTeX.com ]-1 ; 2 [](http://www.rozenblum.com/wp-content/ql-cache/quicklatex.com-64c41bccb0a38f652b7683f5b1cd5a8c_l3.png)
