I – Parité d’une fonction
 est une fonction paire si et seulement si pour tout
est une fonction paire si et seulement si pour tout 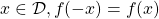 .
. est une fonction impaire si et seulement si pour tout
est une fonction impaire si et seulement si pour tout 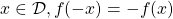 .
.
Exemples :
- La fonction identité définie par :
 , est une fonction impaire.
, est une fonction impaire. - La fonction valeur absolue définie par
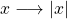 , est une fonction paire.
, est une fonction paire.
 Démonstration : Soit la fonction
Démonstration : Soit la fonction ![]() paire définie sur un ensemble
paire définie sur un ensemble ![]() par
par ![]() , dont voici la courbe représentative.
, dont voici la courbe représentative.
Soient les points ![]() et
et ![]() de la courbe représentative de
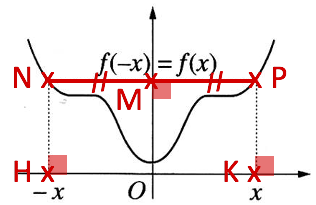
de la courbe représentative de ![]() . les ordonnés de N et P sont égales puisque
. les ordonnés de N et P sont égales puisque ![]() est paire.
est paire.
Calculons les coordonnées de M milieu du segment [NP]. L’abscisse de M vaut ![]() . Ce qui prouve que M est sur l’axe des ordonnées.
. Ce qui prouve que M est sur l’axe des ordonnées.
Soient H et K, les projetés orthogonaux respectifs de N et P. La distance HN est égale à l’ordonnée du point N, ![]() . La distance KP est égale à l’ordonnée de P,
. La distance KP est égale à l’ordonnée de P, ![]() aussi. Par conséquent la droite (NP) est parallèle à la droite (HK) qui est l’axe des abscisses. Comme l’axe des abscisses est perpendiculaire à l’axe des ordonnées, il vient que l’axe des ordonnées et la droite (NP) sont perpendiculaires.
aussi. Par conséquent la droite (NP) est parallèle à la droite (HK) qui est l’axe des abscisses. Comme l’axe des abscisses est perpendiculaire à l’axe des ordonnées, il vient que l’axe des ordonnées et la droite (NP) sont perpendiculaires.
Nous avons donc démontrer que l’axe des ordonnées est perpendiculaire au segment [NP] et passe son milieu. Donc les points N et P sont symétriques par rapport à l’axe des ordonnées.
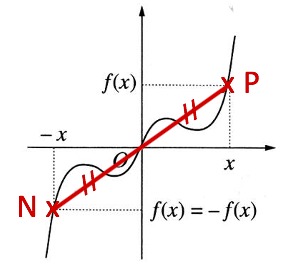 Démonstration : Soit la fonction
Démonstration : Soit la fonction ![]() impaire définie sur un ensemble
impaire définie sur un ensemble ![]() par
par ![]() , dont voici la courbe représentative.
, dont voici la courbe représentative.
Soient les points ![]() et
et ![]() de la courbe représentative de
de la courbe représentative de ![]() . les ordonnés de N et P sont opposées puisque
. les ordonnés de N et P sont opposées puisque ![]() est impaire.
est impaire.
Calculons les coordonnées du milieu du segment [NP]. Son abscisse vaut ![]() . Son ordonnée vaut
. Son ordonnée vaut ![]() . Ce qui prouve que
. Ce qui prouve que ![]() est le milieu du segment [NP] et que par conséquent, N et P sont symétriques par rapport à O.
est le milieu du segment [NP] et que par conséquent, N et P sont symétriques par rapport à O.
II – La fonction carré
- est strictement croissante sur
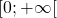
- est strictement décroissante sur
![Rendered by QuickLaTeX.com ]-\infty ; 0 ]](http://www.rozenblum.com/wp-content/ql-cache/quicklatex.com-d869fd330c21f29503be8b5ce2e087d1_l3.png)
- possède un minimum 0 atteint pour
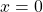
Démonstration :
On rappelle l’identité remarquable : ![]()
Soient ![]() et
et ![]() deux réels positifs tels que
deux réels positifs tels que ![]() . Alors
. Alors ![]() et
et ![]() .
.
Par conséquent ![]() donc
donc ![]() , ce qui donne
, ce qui donne ![]() .
.
Nous venons de démontrer que si ![]() alors
alors ![]() . Ainsi la fonction carré est croissante sur
. Ainsi la fonction carré est croissante sur ![]() .
.
On démontre de façon similaire que la fonction carré est décroissante sur ![]() .
.
Enfin, nous savons que tout carré est positif et ne s’annule que pour le carré de 0. Cela suffit à prouver que la fonction carré possède un minimum 0 atteint pour ![]() .
.
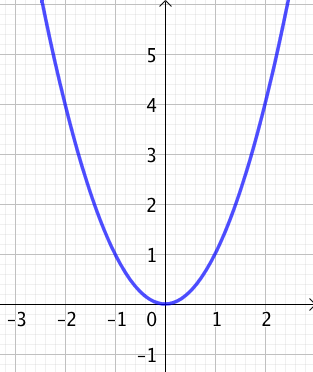
Tableau de variation et courbe représentative
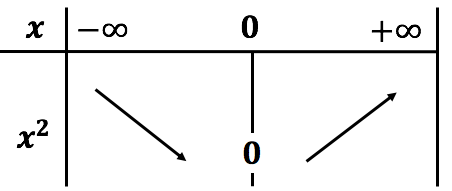
La courbe représentative de la fonction carré est une parabole. Le sommet de la parabole est le point O, origine du repère. |
 |
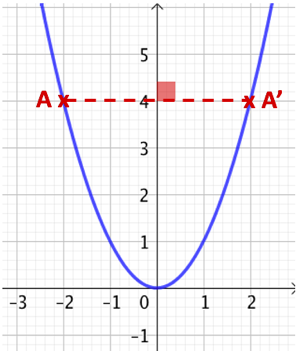 Démonstration : deux nombres opposés ont le même carré :
Démonstration : deux nombres opposés ont le même carré : ![]() .
.
Interprétation géométrique : la courbe représentative de la fonction carré est symétrique par rapport à l’axe des ordonnées.
Exemple : Les points ![]() et
et ![]() sont symétriques par rapport à l’axe des ordonnées.
sont symétriques par rapport à l’axe des ordonnées.
III – La fonction inverse
Démonstration : Soient ![]() et
et ![]() deux nombres réels non nuls.
deux nombres réels non nuls.
![]() .
.
Supposons que ![]() . Alors
. Alors ![]() . Donc le signe de
. Donc le signe de ![]() ne dépend que du signe du dénominateur.
ne dépend que du signe du dénominateur.
Si ![]() et
et ![]() appartiennent à l’intervalle
appartiennent à l’intervalle ![]() , ils sont donc tous les deux négatifs et leur produit est positif.
, ils sont donc tous les deux négatifs et leur produit est positif.
Si ![]() et
et ![]() appartiennent à l’intervalle
appartiennent à l’intervalle ![]() , ils sont donc tous les deux positifs et leur produit est positif.
, ils sont donc tous les deux positifs et leur produit est positif.
Finalement, l’expression ![]() est toujours positive, donc
est toujours positive, donc ![]() est toujours positive, c’est-à-dire que
est toujours positive, c’est-à-dire que ![]() .
.
Partant de l’hypothèse que ![]() , on aboutit à la conclusion que
, on aboutit à la conclusion que ![]() . Cela achève de démontrer que la fonction inverse est strictement décroissante.
. Cela achève de démontrer que la fonction inverse est strictement décroissante.
Tableau de variation et courbe représentative
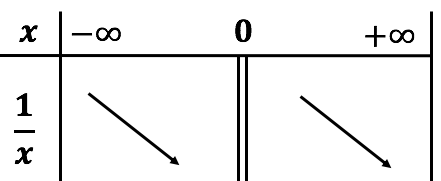
La courbe représentative de la fonction inverse est une hyperbole. Comme la fonction inverse n’est pas définie en 0, sa courbe représentative n’est pas continue : elle composée de deux parties qui ne se rejoignent pas. |
 |
Démonstration : deux nombres opposés ont leurs inverses également opposés.
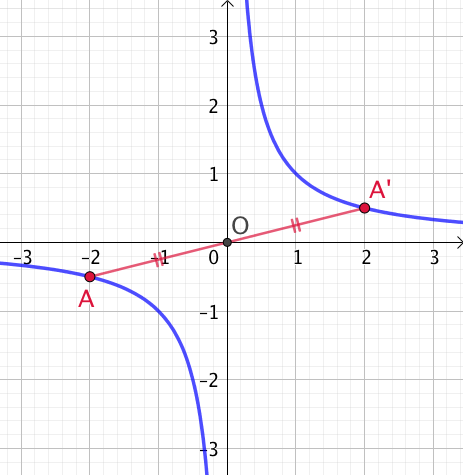
Interprétation géométrique : la courbe représentative de la fonction inverse est symétrique par rapport à l’origine O du repère orthonormé.
Exemple : Dans le figure ci-dessus, les points ![]() et
et ![]() sont symétriques par rapport au point O.
sont symétriques par rapport au point O.
IV – La fonction cube
- est impaire ;
- est strictement croissante sur
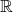 .
.
Démonstration de la parité :
Soit ![]() . La fonction cube est donc impaire.
. La fonction cube est donc impaire.
Démonstration de la monotonie :
1er cas : Soient ![]() et
et ![]() deux réels positifs tels que
deux réels positifs tels que ![]() , alors
, alors ![]() car la fonction carré est croissante sur
car la fonction carré est croissante sur ![]() .
.
Comme ![]() , il vient que
, il vient que ![]() , c’est-à-dire
, c’est-à-dire ![]() .
.
Comme ![]() et que
et que ![]() , il vient que
, il vient que ![]() , c’est-à-dire
, c’est-à-dire ![]() .
.
Nous avons donc obtenu le résultat suivant : ![]() , donc
, donc ![]() .
.
En partant de ![]() , on obtient
, on obtient ![]() . La fonction cube est strictement croissante sur
. La fonction cube est strictement croissante sur ![]() .
.
2ème cas : Soient ![]() et
et ![]() deux réels négatifs tels que
deux réels négatifs tels que ![]() , alors après multiplication des deux membres de l’inégalité par
, alors après multiplication des deux membres de l’inégalité par ![]() , on obtient
, on obtient ![]() .
.
Or ![]() et
et ![]() sont positifs, donc
sont positifs, donc ![]() d’après le résultat précédent.
d’après le résultat précédent.
Donc ![]() , ce qui donne après multiplication des deux membres de l’inégalité par
, ce qui donne après multiplication des deux membres de l’inégalité par ![]() :
: ![]() . La fonction cube est strictement croissante sur
. La fonction cube est strictement croissante sur ![]() .
.
3ème cas : Soient ![]() et
et ![]() deux réels tel que
deux réels tel que ![]() et
et ![]() . Il est évident que
. Il est évident que ![]() . Par ailleurs si
. Par ailleurs si ![]() alors
alors ![]() et si
et si ![]() alors
alors ![]() . Ce qui aboutit à
. Ce qui aboutit à ![]() .
.
Dans ce cas aussi la croissance de la fonction cube est démontrée.
Tableau de variation et courbe représentative
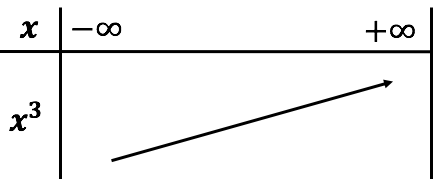 |
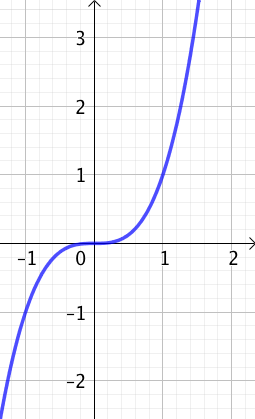 |
V – La fonction racine carrée
Démonstration : Soient ![]() et
et ![]() deux réels, tels que
deux réels, tels que ![]() . Pour démontrer que
. Pour démontrer que ![]() , on va démontrer que
, on va démontrer que ![]() .
.
![]()
Les racines étant toujours positives, ![]() . Par hypothèse
. Par hypothèse ![]() donc
donc ![]() . On obtient ainsi que
. On obtient ainsi que ![]() , c’est-à-dire
, c’est-à-dire ![]() . La fonction racine carrée est donc strictement croissante.
. La fonction racine carrée est donc strictement croissante.
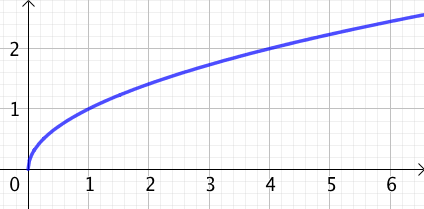
Tableau de variation et courbe représentative
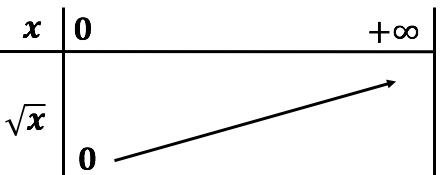 |
 |
