I – Définitions et vocabulaire
 Exemple :
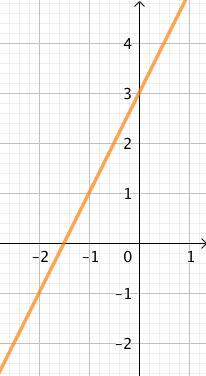
Exemple : ![]() dont la courbe représentative est la courbe ci-ontre.
dont la courbe représentative est la courbe ci-ontre.
Remarque : Le domaine de définition de toutes les fonctions affines est ![]() .
.
- si
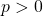 alors
alors  est strictement croissante.
est strictement croissante. - si
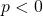 alors
alors  est strictement décroissante.
est strictement décroissante. - si
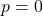 alors
alors  est constate : pour tout réel
est constate : pour tout réel 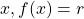 .
.
Démonstrations :
On suppose que ![]()
Soit ![]() et
et ![]() deux réels tels que
deux réels tels que ![]() . Alors
. Alors ![]() car
car ![]() . Donc
. Donc ![]() . On en conclut que
. On en conclut que ![]() . La fonction
. La fonction ![]() est strictement croissante.
est strictement croissante.
On suppose que ![]()
Soit ![]() et
et ![]() deux réels tels que
deux réels tels que ![]() . Alors
. Alors ![]() car
car ![]() et on sait que multiplier les deux membres d’une inégalité par un nombre négatif, inverse le sens de l’inégalité. Donc
et on sait que multiplier les deux membres d’une inégalité par un nombre négatif, inverse le sens de l’inégalité. Donc ![]() . On en conclut que
. On en conclut que ![]() . La fonction
. La fonction ![]() est strictement décroissante.
est strictement décroissante.
On suppose que ![]() . Alors pour réel
. Alors pour réel ![]() .
. ![]() est bien une fonction constante et sa courbe représentative est une droite parallèle à l’axe des abscisses et passant par le point de coordonnées
est bien une fonction constante et sa courbe représentative est une droite parallèle à l’axe des abscisses et passant par le point de coordonnées ![]() .
.
Exemple :
 |
 |
 |
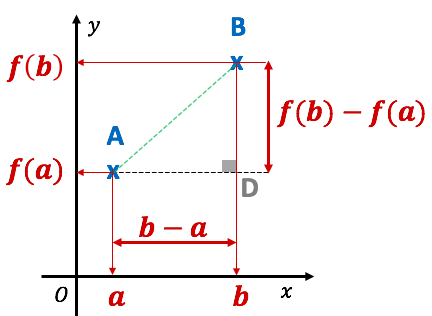 Démonstration :
Démonstration :
Soient deux réels différents ![]() et
et ![]() .
.
![]()
![]() .
.
![]()
![]() .
.
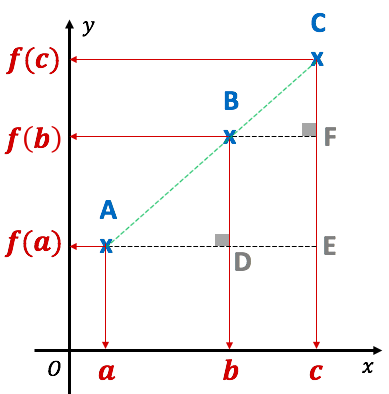 Démonstration :
Démonstration :
Soient ![]() et
et ![]() deux réels donnés et soit la fonction affine
deux réels donnés et soit la fonction affine ![]()
Soient trois réels ![]() ,
, ![]() et
et ![]() , tels que
, tels que ![]() .
.
Les points ![]() ,
, ![]() et
et ![]() appartiennent à la courbe représentative de la fonction affine
appartiennent à la courbe représentative de la fonction affine ![]() .
.
Pour démontrer que la courbe représentative de ![]() est une droite, il suffit de montrer que les points
est une droite, il suffit de montrer que les points ![]() ,
, ![]() et
et ![]() sont alignés.
sont alignés.
Pour cela démontrer cette égalité de distance : ![]() à l’aide du théorème de Pythagore.
à l’aide du théorème de Pythagore.
On rappelle un calcul utilisé dans la démonstration précédente : ![]()
![]()
Par conséquent ![]() .
.
Comme ![]() , alors
, alors ![]() , donc
, donc ![]()
Finalement ![]() .
.
On démontre de la même façon que ![]() et
et ![]() .
.
![]()
Le nombre réel ![]() est le coefficient directeur (ou pente) de la droite représentative de la fonction affine.
est le coefficient directeur (ou pente) de la droite représentative de la fonction affine.
Cela nous permet de retrouver un langage familier :
- si la pente de la droite est positive (elle monte), alors la fonction affine est strictement croissante.
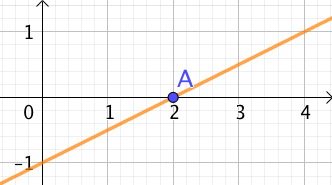
- si la pente de la droite est négative (elle descend), alors la fonction affine est strictement décroissante.
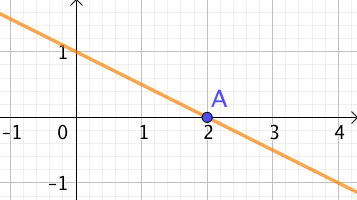
- Si la pente est nulle, la droite est horizontale et la fonction affine est constante.
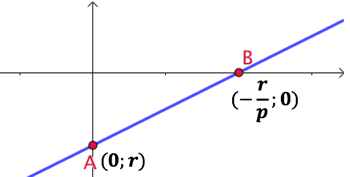 Interprétation graphique : la droite représentative de la fonction affine
Interprétation graphique : la droite représentative de la fonction affine ![]() coupe
coupe
- l’axe des ordonnées au point de coordonnées
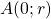
- l’axe des abscisses au point de coordonnées
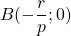
Démonstrations :
![]()
![]()
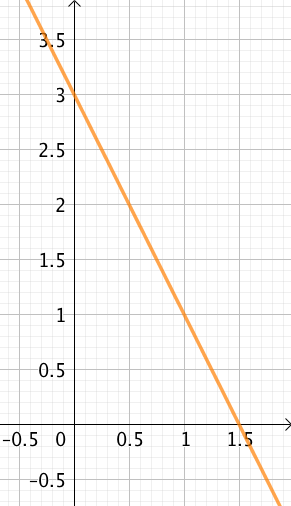 Exemple : En utilisant la représentation graphique d’une fonction affine, on va retrouver la définition de cette fonction.
Exemple : En utilisant la représentation graphique d’une fonction affine, on va retrouver la définition de cette fonction.
Soit la fonction affine ![]() ,
, ![]() et
et ![]() étant deux réels donnés, associée à cette droite.
étant deux réels donnés, associée à cette droite.
Le point de coordonnées ![]() appartient à cette droite., donc
appartient à cette droite., donc ![]() . Or nous savons que
. Or nous savons que ![]() . Par conséquent
. Par conséquent ![]() .
.
Nous savons que la fonction s’annule pour ![]() . Or la droite coupe l’axe des abscisses au point de coordonnées
. Or la droite coupe l’axe des abscisses au point de coordonnées ![]() . Par conséquent
. Par conséquent ![]() .
.
Comme ![]() , il vient
, il vient ![]() , soit
, soit ![]() donc
donc ![]() .
.
Conclusion : la fonction ![]() est définie par
est définie par ![]() .
.
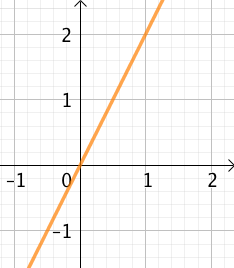
II – Fonctions linéaires
Autrement dit, la définition d’une fonction linéaire est de la forme : ![]() , où
, où ![]() .
.
 Démonstration : Soit la fonction linéaire définie par :
Démonstration : Soit la fonction linéaire définie par : ![]() , où
, où ![]() . Alors
. Alors ![]() .
.
Exemple : ![]()
III – Signe d’une fonction affine
Soient ![]() et
et ![]() deux réels donnés et soit la fonction affine
deux réels donnés et soit la fonction affine ![]() .
.
Nous savons que ![]() , Interprétation graphique : la droite représentative de
, Interprétation graphique : la droite représentative de ![]() coupe l’axe des abscisses au point d’abscisse
coupe l’axe des abscisses au point d’abscisse ![]() .
.
Donc ![]() change de signe de part et d’autre de ce point. Ce qui donne les résultats suivants :
change de signe de part et d’autre de ce point. Ce qui donne les résultats suivants :
| La fonction affine est croissante | 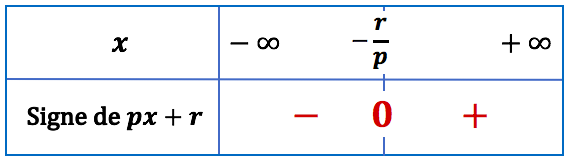 |
|
| La fonction affine est décroissante | 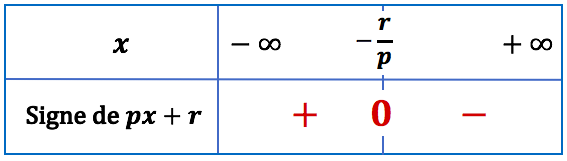 |
|
| La fonction affine est constante : |
La fonction |
Remarque : on retrouve ainsi les résultats sur le signe d’un expression du premier degré.
IV – Signe du produit d’expressions du premier degré
Étant données quatre nombres réels ![]() , on veut déterminer le signe de l’expression
, on veut déterminer le signe de l’expression ![]() .
.
- On étudie le signe de l’expression
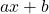
- On étudie le signe de l’expression
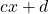
- On rassemble toutes les résultats obtenus dans un même tableau
- Le signe du produit
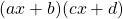 s’obtient à l’aide de la règle des signes.
s’obtient à l’aide de la règle des signes.
Exemple : Étude du signe de ![]()
| Signe de |
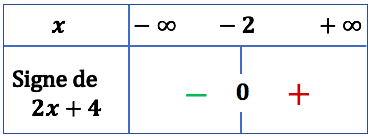 |
| Signe de |
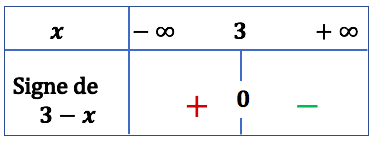 |
| Signe de La première ligne contient les deux valeurs de |
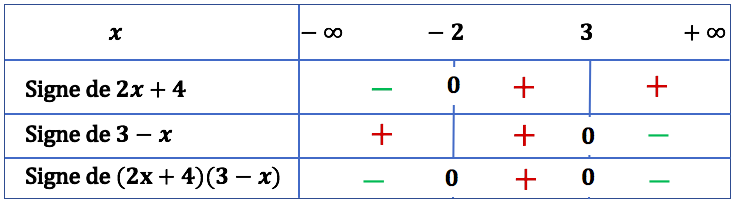 |
Interprétation : Le tableau précédent nous permet d’écrire que ![]() si
si ![]()
V – Signe du quotient d’expressions du premier degré
Étant données quatre nombres réels ![]() , on veut déterminer le signe de l’expression
, on veut déterminer le signe de l’expression ![]() .
.
- Même méthode que pour le signe d’un produit
- On place une double barre en dessous de la valeur de
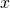 qui annule le dénominateur
qui annule le dénominateur 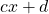 , c’est-à-dire pour
, c’est-à-dire pour 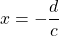
Exemple : Étude du signe de ![]()
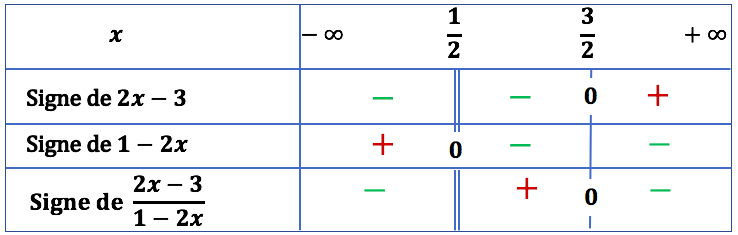
On a placé une double barre sous ![]() pour indiquer que le quotient n’est pas défini pour cette valeur qui annule son dénominateur.
pour indiquer que le quotient n’est pas défini pour cette valeur qui annule son dénominateur.
Interprétation : Le tableau précédent nous permet d’écrire que ![]() si
si ![]() . Attention, le crochet est ouvert du côté de
. Attention, le crochet est ouvert du côté de ![]() .
.
