APPLICATIONS
Soient ![]()
![]()
![]()
Remarque : Si ![]() est injective alors la dernière inclusion est une égalité.
est injective alors la dernière inclusion est une égalité.
Cas particulier : ![]() et
et ![]() sont des ensembles finis.
sont des ensembles finis.
![]()
![]()
Si ![]() et
et ![]() alors
alors
- Le nombre d’applications différentes de
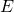 dans
dans 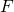 est
est 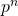
- Le nombre d’injections de
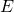 dans
dans 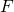 est
est 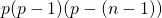
- Le nombre de bijections de
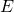 dans
dans 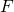 est
est 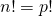
MONOTONIE
- La somme de deux fonctions (dé)croissantes est une fonction (dé)croissante.
- Le produit de deux fonctions croissantes et positives est une fonction croissante.
- La composée de deux fonctions croissantes ou de deux fonctions décroissantes est une fonction croissante.
- La composée d’une fonction croissante et d’une fonction décroissante est une fonction décroissante.
- Une fonction strictement monotone sur un intervalle est injective.
COURBES REPRÉSENTATIVES ET SYMÉTRIE
Soit une fonction ![]() dont la courbe représentative est
dont la courbe représentative est ![]() .
.
- La droite d’équation
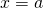 est un axe de symétrie de
est un axe de symétrie de 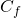 si et seulement si
si et seulement si 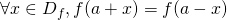 .
. - Le point de coordonnées
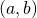 est un centre de symétrie de
est un centre de symétrie de 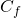 si et seulement si
si et seulement si 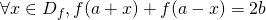 .
.
Dit autrement : on définit les fonctions suivantes : ![]()
- La droite d’équation
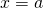 est un axe de symétrie de
est un axe de symétrie de 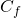 si et seulement si la fonction
si et seulement si la fonction 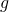 est paire.
est paire. - Le point de coordonnées
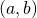 est un centre de symétrie de
est un centre de symétrie de 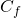 si et seulement si la fonction
si et seulement si la fonction 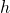 est impaire.
est impaire.
LIMITES
![]()
Si ![]() alors f est bornée au voisinage de a. Si de plus l est non nul alors f garde le signe de l et ne s’annule pas au voisinage de a.
alors f est bornée au voisinage de a. Si de plus l est non nul alors f garde le signe de l et ne s’annule pas au voisinage de a.
Si ![]() alors f est strictement positive et non majorée au voisinage de a.
alors f est strictement positive et non majorée au voisinage de a.
![]()
Théorème de la limite monotone : f définie et monotone sur ![]() alors
alors ![]() , f admet une limite à gauche et à droite en c.
, f admet une limite à gauche et à droite en c.
LIMITES USUELLES
![]()
![]()
![]()
Asymptotes et branches paraboliques :
![]()
![]()
![]()
Remarque : les réciproques de ces trois implications sont vraies.
CONTINUITÉ
Continuité et limite de suite.
Soit ![]() adhérent à
adhérent à ![]() .
.
![]()
![]()
Théorème de Bolzano : ![]() continue sur
continue sur ![]()
Théorème des valeurs intermédiaires : ![]() continue sur
continue sur ![]() et soit
et soit ![]() compris entre
compris entre ![]() et
et ![]() alors
alors ![]() tel que
tel que ![]() . Le nombre
. Le nombre ![]() est unique si
est unique si ![]() est strictement monotone sur
est strictement monotone sur ![]() .
.
Théorème de Weierstrass : ![]() continue sur
continue sur ![]() . Alors
. Alors ![]() tels que
tels que ![]() . Autrement dit, toute fonction continue sur un intervalle y est bornée et atteint ses bornes.
. Autrement dit, toute fonction continue sur un intervalle y est bornée et atteint ses bornes.
Conséquence : l’image d’un intervalle fermé par une fonction continue est un intervalle fermé.
Autres propriétés :
- Si l’image d’un intervalle par une fonction monotone est un intervalle, alors la fonction est continue sur cet intervalle.
- Une fonction injective et continue sur un intervalle est strictement monotone.
ÉQUIVALENCES
Notations de Landau
![]() et
et ![]() sont des fonctions définies sur
sont des fonctions définies sur ![]() .
. ![]() .
. ![]() ne s’annule pas au voisinage de
ne s’annule pas au voisinage de ![]() sauf éventuellement en
sauf éventuellement en ![]() .
.
![]()
![]()
![]()
Équivalences
![]()
![]()
![]()
Propriétés
![]()
![]()
![]()
![]()