I – Vocabulaire de base
1) Droite, demi-droite et segment
| Figure | Notation | Signification |
| Lire : « segment [AB] ».
C’est le segment d’extrémités A et B. |
||
| AB | La longueur d’un segment est la distance qui séparent les deux extrémités de ce segment. | |
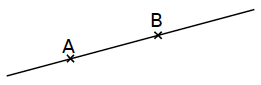 |
Lire : « droite (AB) ».
C’est la droite qui passe par les points A et B. |
|
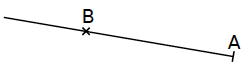 |
Lire : « demi-droite [AB) ».
C’est la demi-droite d’origine A passant par le point B. |
|
 |
|
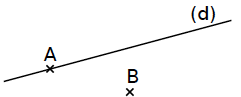
Le point A appartient à la droite (d).
Le point B n’appartient pas à la droite (d). |
2) Points alignés
- Par un point, il passe une infinité de droites.
- Deux points sont toujours alignés.
- Par deux points, il ne passe qu’une seule droite.
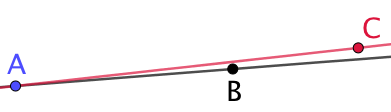
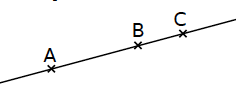 Exemple : Les points A, B et C sont alignés.
Exemple : Les points A, B et C sont alignés.
II – Droites sécantes et angles
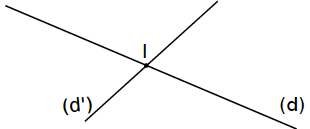 Exemple : Le point I est le point d’intersection des droites (d) et (d’).
Exemple : Le point I est le point d’intersection des droites (d) et (d’).
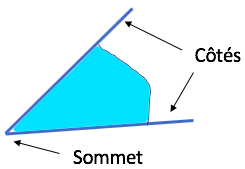 Un angle est une portion de plan délimitée par deux demi-droites ayant la même origine.
Un angle est une portion de plan délimitée par deux demi-droites ayant la même origine.- Les deux demi-droites s’appellent les côtés de l’angle.
- L’origine commune des deux demi-droites s’appelle le sommet de l’angle.
- La mesure d’un angle est l’écartement de ses deux côtés.
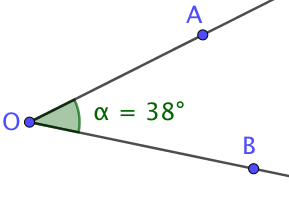 L’angle de sommet O et de côté [OA) et [OB) se note
L’angle de sommet O et de côté [OA) et [OB) se note La lettre du milieu représente le sommet de l’angle.
III – Droites parallèles
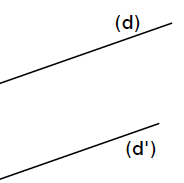 Exemple : Les droites (d) et (d’) sont parallèles. Elles ne se coupent pas. Elles n’ont pas de point d’intersection.
Exemple : Les droites (d) et (d’) sont parallèles. Elles ne se coupent pas. Elles n’ont pas de point d’intersection.
On note : (d) // (d’)
 |
 |
| Les droites (AB) et (AC) ont un point en commun qui est A. Elles ne sont pas parallèles. | La seule possibilité pour que deux droites soient parallèles et qu’elles possèdent au moins un point en commun,est qu’elles soient confondues. |
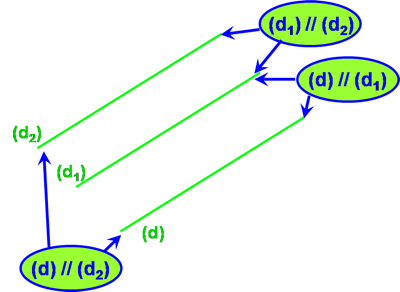
Exemple :
- On sait que (d2) est parallèle à (d1) et que (d) est aussi parallèle à (d1).
- On en déduit donc que (d) est parallèle à (d2).
Construction d’une droite parallèle à une autre droite
| On va tracer la droite parallèle à la droite |
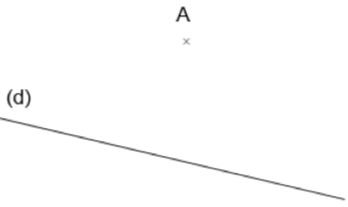 |
| On choisit deux points quelconques On trace un arc de cercle de centre |
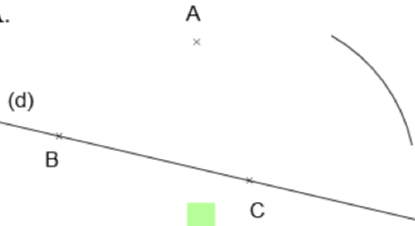 |
| On trace un arc de cercle de centre |
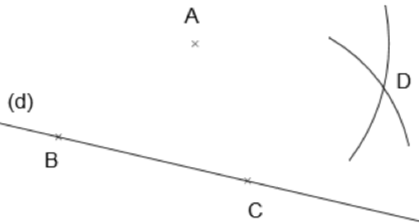 |
| Soit La droite |
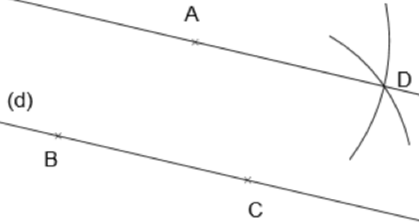 |
IV – Droites perpendiculaires
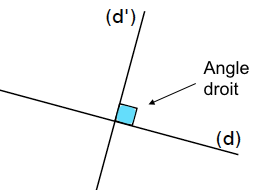 Exemple :
Exemple :
La droite (d’) est perpendiculaire à la droite (d).
On peut aussi dire que la droite (d) est perpendiculaire à la droite (d’).
On note : ![]() pour (d) perpendiculaire à (d’).
pour (d) perpendiculaire à (d’).
Remarque : Deux droites perpendiculaires forment entre elle quatre angles droits.
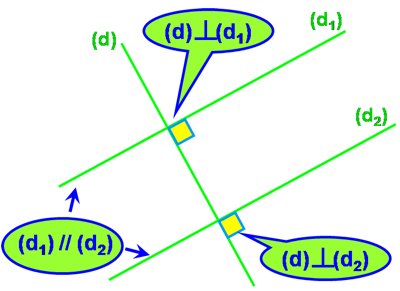 Exemple :
Exemple :
- On sait que (d1) est perpendiculaire à (d) et que (d2) est aussi perpendiculaire à (d).
- Alors (d1) et (d2) sont parallèles.
Exemple : On utilise à nouveau la figure précédente.
- On sait que (d1) et (d2) sont parallèles et que (d) est perpendiculaire à (d1).
- Alors (d) est aussi perpendiculaire à (d2).
Construction de la perpendiculaire à une droite
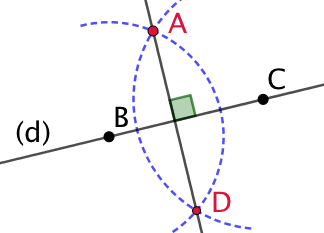
| On va tracer la droite perpendiculaire à (d) qui passe par le point A. | 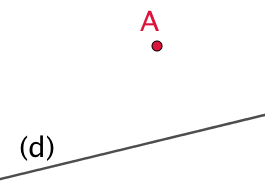 |
| On choisit deux points quelconques B et C sur la droite (d). | 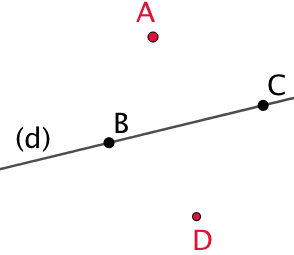 |
| On trace un arc de cercle de centre B passant par A.
|
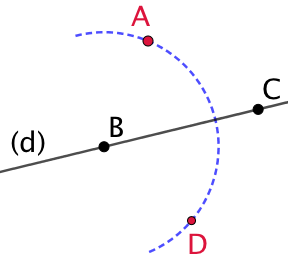 |
| On trace un arc de cercle de centre C passant par A. | 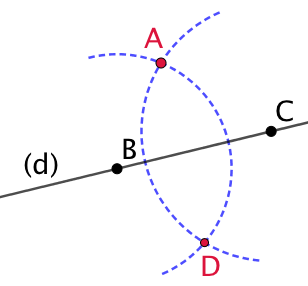 |
| Ces arcs de cercle se croisent au point D. La droite (AD) est la droite perpendiculaire à (d) et passant par A.
On code la figure pour indiquer que les deux droites sont perpendiculaires. |
 |
V – Angles et droites parallèles
1) Angles adjacents
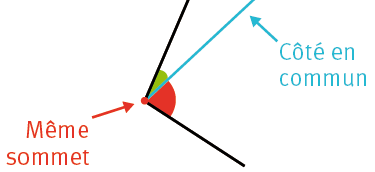 Deux angles adjacents sont deux angles qui ont un sommet commun, un côté commun et qui sont situés de part et d’autre de ce côté commun.
Deux angles adjacents sont deux angles qui ont un sommet commun, un côté commun et qui sont situés de part et d’autre de ce côté commun.
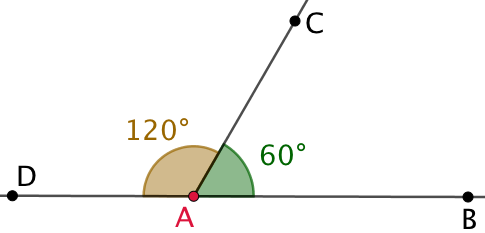 Deux angles adjacents dont la somme des mesures est égales à 180° sont appelés supplémentaires.
Deux angles adjacents dont la somme des mesures est égales à 180° sont appelés supplémentaires.
Deux angles supplémentaires forment ensemble un angle plat.
Exemple : ![]() °.
°.
2) Angles opposés par le sommet
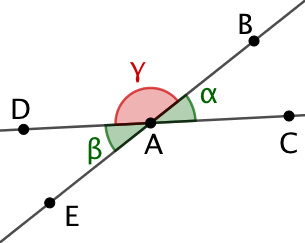 Deux angles sont opposés par le sommet lorsqu’ils ont le même sommet et des côtés dans le prolongement l’un de l’autre.
Deux angles sont opposés par le sommet lorsqu’ils ont le même sommet et des côtés dans le prolongement l’un de l’autre.
Dans la figure de droite, les deux angles dessinés en vert ![]() et
et ![]() sont opposés par le sommet A.
sont opposés par le sommet A.
De même, les angles ![]() et
et ![]() sont opposés par le sommet A.
sont opposés par le sommet A.
Avant d’aller plus loin, il faut comprendre la propriété suivante illustrée par les deux dessins ci-dessous :
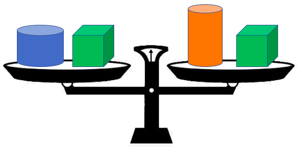
| Imaginons que nous possédons une balance à plateaux et trois objets : un cylindre bleu, un cylindre orange et deux cubes verts de même poids.
Nous posons sur le plateau gauche le cylindre bleu et un cube vert, et sur le plateau droit, le cylindre orange et l’autre cube vert. Nous constatons alors que la balance est équilibrée. la somme des poids du cylindre bleu et du cube vert est égale à la somme des poids du cylindre orange et du cube vert. |
 |
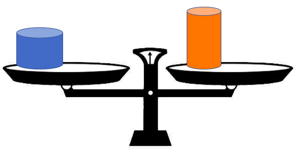
| Que se passe-t-il si on retire des plateaux les deux cubes verts identiques ?
On constate évidemment que la balance reste équilibrée. C’est-à-dire que les deux cylindres ont le même poids. |
 |
Si nous traduisons cela en langage mathématique, cela donne : Si trois nombres ![]() sont tels que
sont tels que ![]() , alors
, alors ![]() . Nous allons utiliser cette propriété pour la démonstration suivante.
. Nous allons utiliser cette propriété pour la démonstration suivante.
Démonstration : En s’appuyant sur la figure ci-dessus, on observe que les points B, A et E sont alignés. Donc les angles ![]() et
et ![]() sont supplémentaires. Ce qui donne l’égalité :
sont supplémentaires. Ce qui donne l’égalité : ![]() .
.
On observe aussi que les points C, A et D sont alignés. Donc les angles ![]() et
et ![]() sont supplémentaires. Ce qui donne l’égalité :
sont supplémentaires. Ce qui donne l’égalité : ![]() .
.
SI ![]() et si
et si ![]() alors
alors ![]() . Conclusion :
. Conclusion : ![]() . Les deux angles opposés ont la même mesure.
. Les deux angles opposés ont la même mesure.
3) Angles correspondants, alternes-internes
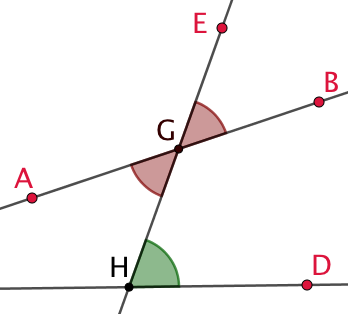 Deux angles formés par deux droites coupées par une droite sécante sont dits alternes-internes si :
Deux angles formés par deux droites coupées par une droite sécante sont dits alternes-internes si :
- ils sont situés de part et d’autre de la droite sécante ;
- ils sont situés entre les deux droites ;
- ils ne sont pas adjacents.
Exemple : Les deux droites (AB) et (HD) sont coupées par une droite sécante (EG). Les angles ![]() et
et ![]() sont des angles alternes-internes.
sont des angles alternes-internes.
- ils sont situés du même côté de la droite sécante ;
- Leurs sommets sont les deux points d’intersection des deux droites avec la droite sécantes.
Exemple : Dans la figure précédente, les angles ![]() et
et ![]() sont des angles correspondants.
sont des angles correspondants.
- Si deux droites forment avec une même droite sécante des angles alternes-internes de même mesure, alors ces droites sont parallèles.
- Si deux droites forment avec une même droite sécante des angles correspondants de même mesure, alors ces droites sont parallèles.
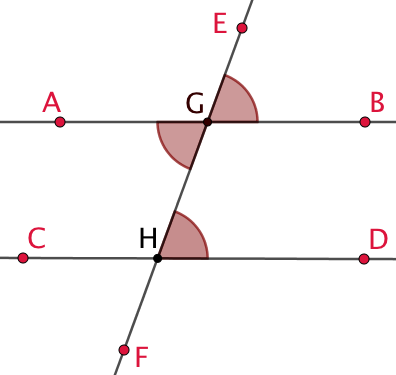 Exemple :
Exemple :
Les angles alternes-internes ![]() et
et ![]() sont de même mesure. Donc les droites (AB) et (CD) sont parallèles.
sont de même mesure. Donc les droites (AB) et (CD) sont parallèles.
Les angles correspondants ![]() et
et ![]() sont de même mesure. Donc les droites (AB) et (CD) sont parallèles.
sont de même mesure. Donc les droites (AB) et (CD) sont parallèles.
- Si deux droites sont parallèles et forment avec une même droite sécante des angles alternes-internes, alors ces angles ont la même mesure.
- Si deux droites sont parallèles et forment avec une même droite sécante des angles correspondants, alors ces angles ont la même mesure.
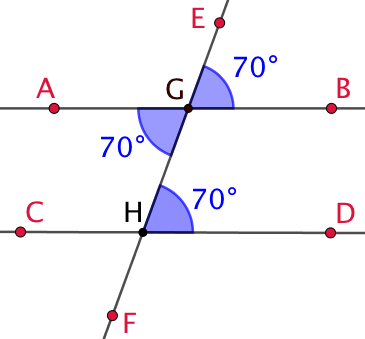 Exemple :
Exemple :
Les droites (AB) et (CD) sont parallèles. Alors si on trace une droite sécante (EF) à ces deux droites, on forme des angles alternes-internes et des angles correspondants ayant tous la même mesure :
![]()
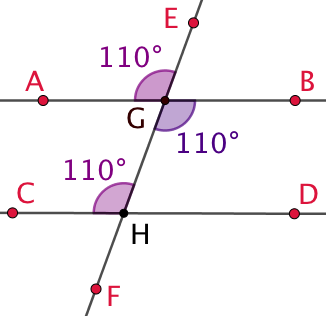 On observe également que les angles alternes-internes
On observe également que les angles alternes-internes ![]() et
et ![]() sont de même mesure.
sont de même mesure.
Pour les mêmes raisons, les angles correspondants ![]() et
et ![]() sont de même mesure.
sont de même mesure.
![]()
EXERCICES
- 1 / 101 : Retrouver des droites parallèles et perpendiculaires
- 2 / 101 : théorème
- 4 / 101 : Mesures d’angles
- 5 / 101 : droites parallèles (triangle équilatéral)
- 11 / 102 : tracer des droites
- 15 / 103 : construction et propriété
- 17 / 103 : devinette
- 27 / 105 : droites parallèles et angles
- 31 / 105 : mesures d’angles
- 33 / 105 : mesures d’angles
- 36 / 106 : mesure d’angles dans deux triangles
