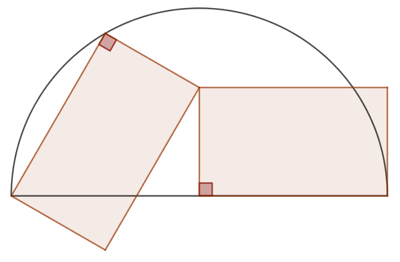
Comment positionner deux rectangles isométriques dans un demi-cercle de telle manière qu’un l’un soit aligné à droite sur un diamètre du demi cercle et que l’autre touche le premier rectangle en un sommet et le demi-cercle en deux autres sommets, comme indiqué sur la figure de droite ?
Résultat n°1 : le grand côté des rectangle est égal au rayon du demi-cercle
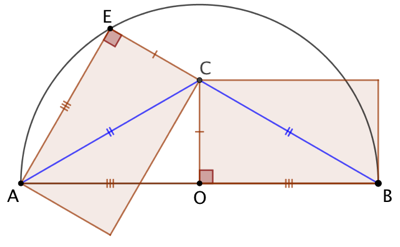 Les deux rectangles sont isométriques donc leurs diagonales ont la même longueur. Ainsi AC = CB. Par conséquent C appartient à la médiatrice de [AB] qui est la droite (CO). Ce qui démontre que la longueur OB est le rayon du demi-cercle.
Les deux rectangles sont isométriques donc leurs diagonales ont la même longueur. Ainsi AC = CB. Par conséquent C appartient à la médiatrice de [AB] qui est la droite (CO). Ce qui démontre que la longueur OB est le rayon du demi-cercle.
Résultat n°2 : Les points E, C et B sont alignés
Comme E est sur le cercle de diamètre AB, le triangle AEB est rectangle en E. Par ailleurs l’angle ![]() est droit puisque nous avons un rectangle. Ce qui implique que les points E, C et B sont alignés.
est droit puisque nous avons un rectangle. Ce qui implique que les points E, C et B sont alignés.
Résultat n°3 : ![]()
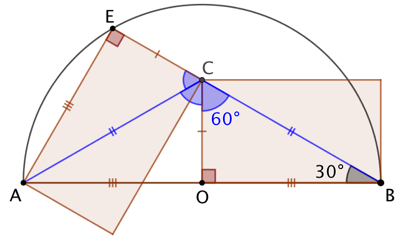 Les triangles CEA, CAO et COB sont isométriques. Donc
Les triangles CEA, CAO et COB sont isométriques. Donc ![]() et leur somme fait 180°. Par conséquent chacun de ces angles mesure 60°. Ce qui permet de conclure que
et leur somme fait 180°. Par conséquent chacun de ces angles mesure 60°. Ce qui permet de conclure que ![]()