Deux triangles, dont les bases ont la même longueur et dont les sommets sont portés par une droite parallèle à leurs bases, ont la même aire.
Explications :
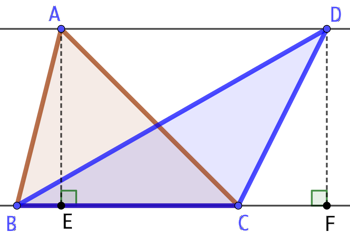
Les triangles ABC et DBC ont une base commune. Leurs sommets A et D appartiennent à une droite parallèle à (BC). Donc leurs hauteurs [AE] et [DF] ont la même longueur. Étant donné que l’aire d’un triangle est le demi produit de sa base par sa hauteur, les deux triangles ABC et DBC ont la même aire.
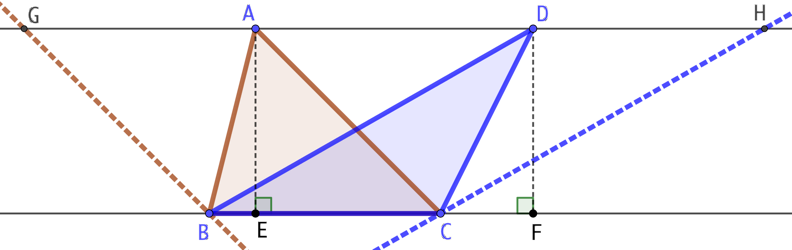Remarque : Euclide s’appuie sur le fait que deux parallélogrammes de même base ont la même aire (Proposition I.35). Il construit les droites (BG) parallèle à (CA) et (CH) parallèle à (BD) pour créer deux parallélogrammes GBCA et DBCH de même aire et d’aire double de celles des triangles.
Remarque : Il s’agit de la proposition I.37 des Éléments d’Euclide. La proposition I.38 est très proche. Les propositions I.39 et I.40 sont les réciproques qui se démontrent de manière évidente à l’aide d’un raisonnement par l’absurde.
