Exercice n°A
Un sac opaque contient 50 jetons numérotés de 0 à 49. On prélève au hasard un jeton de ce sac et on note le numéro du jeton obtenu. On considère les évènements :
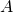 : « Le numéro obtenu est divisible par 9 »
: « Le numéro obtenu est divisible par 9 »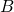 : « Le numéro obtenu est un multiple de 8 »
: « Le numéro obtenu est un multiple de 8 »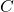 : « Le numéro obtenu est un nombre premier »
: « Le numéro obtenu est un nombre premier »
Déterminer la probabilité de chacun des évènement suivants :
Réponses :
a) ![]() Donc
Donc ![]() .Alors
.Alors ![]()
b) ![]() . Donc
. Donc ![]() . Alors
. Alors ![]()
c) ![]() . Donc
. Donc ![]()
d) ![]() . Donc
. Donc ![]()
e) Les évènements B et C n’ont aucune issue en commun car un nombre premier ne peut pas être un multiple de 8. Donc ![]()
f) Les évènements A et C n’ont aucune issue en commun car un nombre premier ne peut pas être divisible par 9. Donc ![]()
Exercice n°B
Nicolas est un astronome amateur. Il observe le ciel tous les soirs. Il constate qu’il a quatre chances sur cinq de voir Mars, une chance sur trois de voir Jupiter et trois chances sur dix de voir les deux planètes. Quelle est la probabilité que Nicolas ne voit aucune planète ce soir ?
On considère les deux évènements suivants :
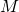 = « Voir la planète Mars ce soir ». Alors
= « Voir la planète Mars ce soir ». Alors 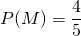
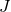 = « Voir la planète Jupiter ce soir ». Alors
= « Voir la planète Jupiter ce soir ». Alors 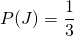
![]() est l’évènement « Voir les deux planètes ce soir ». Alors
est l’évènement « Voir les deux planètes ce soir ». Alors ![]()
On nous demande la probabilité de l’évènement A : « Ne voir aucune planète ce soir ». L’évènement contraire à A, noté ![]() , est « Voir au moins une des deux planètes ce soir ». On en déduit que
, est « Voir au moins une des deux planètes ce soir ». On en déduit que ![]() .
.
![]()
Conclusion ![]()
Exercice n°C
Dans un lycée de 1100 élèves, un sondage a été réalisé pour savoir dans quels pays, ils ont déjà séjourné. En voici les résultats :
- 20% des élèves ont séjourné en Allemagne, 28% en Espagne et 33% au Royaume-uni;
- 15% des élèves ayant séjourné en Allemagne, ont également séjourné au Royaume-uni;
- 18 élèves ont uniquement séjourné en Espagne et en Allemagne;
- Parmi ceux ayant déjà séjourné en Espagne, 26 élèves sont allés également au Royaume-uni;
- 1% des élèves ont séjourné dans ces trois pays.
On choisit un élève au hasard. On note :
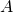 l’évènement « à déjà séjourné en Allemagne »
l’évènement « à déjà séjourné en Allemagne »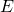 l’évènement « à déjà séjourné en Espagne »
l’évènement « à déjà séjourné en Espagne »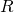 l’évènement « à déjà séjourné au Royaume-uni »
l’évènement « à déjà séjourné au Royaume-uni »
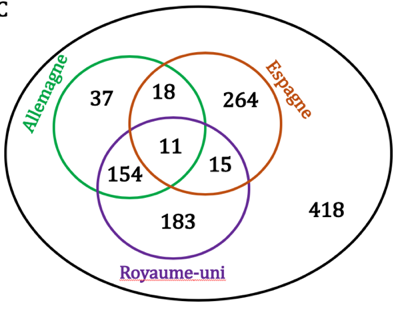 1) Représenter la situation à l’aide d’un diagramme de Venn.
1) Représenter la situation à l’aide d’un diagramme de Venn.
- 1% de élèves dans les 3 pays, soit 11 à l’intersection des 3 ovales.
- 15% des élèves en Allemagne et au R.U., soit 165. On retire les 11 également en Espagne, pour aboutir à 154.
- 18 élèves en espagne et Allemagne uniquement.
- 26 en Espagne et au R.U. On retire les 11 également en Allemagne pour aboutir à 15.
- On complète facilement avec les informations restantes : 20% des élèves ont séjourné en Allemagne, 28% en Espagne et 33% au Royaume-uni;
- On n’oublie les 418 qui n’ont été dans aucun de ces trois pays.
2) Déterminer la probabilité que l’élève :
a) ait déjà séjourné en Allemagne. ![]()
b) n’ai séjourné dans aucun de ces trois pays. ![]()
c) ai séjourné uniquement au Royaume-Uni. ![]()
d) ai séjourné uniquement dans un des trois pays. ![]()
3) Calculer les probabilités de ![]() et
et ![]() .
.
![]()
4) Calculer les probabilités ![]() et
et ![]() .
.
![]()
Exercice n°D
Jean possède un dé pipé. Il lui semble que la face 6 tombe trois fois plus que les autres faces.
1) Proposer une loi de probabilité pour modéliser cette expérience aléatoire.
Supposons que la probabilité de chacune des faces 1, 2, 3, 4 ou 5 soit ![]() . Alors d’après l’énoncé, la probabilité que la face soit 6 est
. Alors d’après l’énoncé, la probabilité que la face soit 6 est ![]() .
.
On sait que la somme des probabilités de toutes les issues d’une expérience aléatoire est 1. Donc ![]() , soit
, soit ![]() , ce qui donne
, ce qui donne ![]() . La loi de probabilité est donc :
. La loi de probabilité est donc :
| 1 | 2 | 3 | 4 | 5 | 6 |
2) Déterminer la probabilité que le résultat d’un lancer du dé soit pair.
L’évènement « lancer du dé pair » est ![]() . Sa probabilité est la somme des probabilités de ses issues, soit
. Sa probabilité est la somme des probabilités de ses issues, soit ![]() .
.
