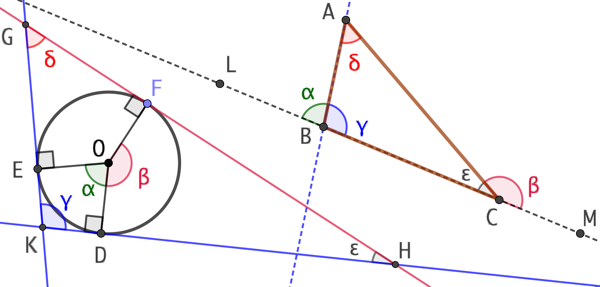
On donne un cercle de centre O et un triangle ABC. On cherche à construire un triangle GKH semblable à ABC et circonscrit au cercle de centre O.
Construction :
- On choisit un point D quelconque sur le cercle et on trace la tangente au cercle en D.
- On prolonge le côté [BC] du côté de B et on pose
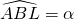. On place le point E sur le cercle de telle sorte que 
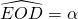. - On trace la tangente au cercle en E. Soit K le point d’intersection de cette tangente avec la tangente en D.
- On prolonge le côté [BC] du côté de C et on pose
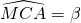. On place le point F sur le cercle de telle sorte que 
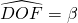. - On trace la tangente au cercle en F. Elle coupe les deux premières tangentes en G et H. Le triangle recherché est GKH.
Explications :
La droite (KH) est la tangente au cercle en D donc elle est perpendiculaire à (OD). Pour la même raison la droite (GK) est perpendiculaire à (OE). Donc le quadrilatère OEKD possède deux angles droits. Sachant que la somme des angles d’un quadrilatère est égale à 
, il vient que 
. Or dans le triangle ABC, 
. Par conséquent 
.
En appliquant le même type de raisonnement au quadrilatère ODHF, on montre que 
.
Donc nécessairement 
et les triangles ABC et GKH sont semblables. Par ailleurs, par construction, GKH est circonscrit au cercle de centre O.
Remarque : Il s’agit de la proposition IV.3 des Élément d’Euclide.
