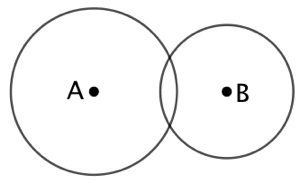
Soient un cercle de centre A et de rayon ![]() et un cercle de centre B et de rayon
et un cercle de centre B et de rayon ![]() . On veut tracer un cercle de rayon
. On veut tracer un cercle de rayon ![]() et tangent aux deux autres cercles.
et tangent aux deux autres cercles.
 |
 |
 |
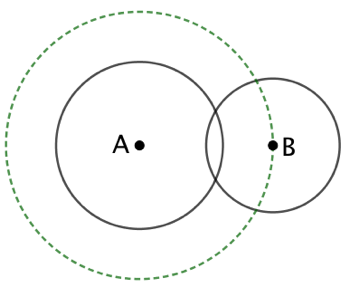
| Si le cercle recherché de centre C est tangent au cercle de centre A et de rayon |
||
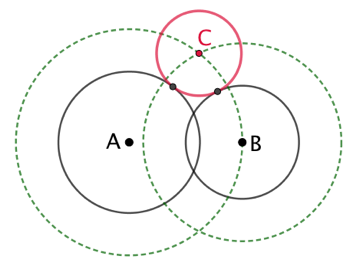 |
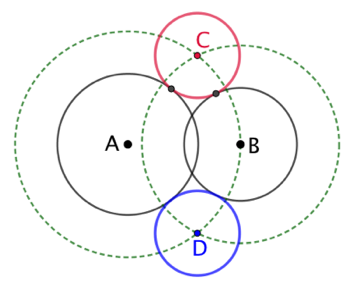 |
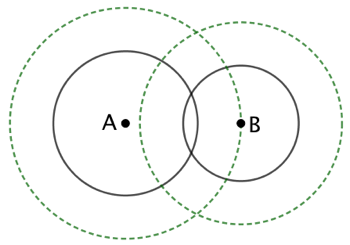
Si le cercle recherché de centre C est tangent au cercle de centre B et de rayon Les deux cercles de rayon |
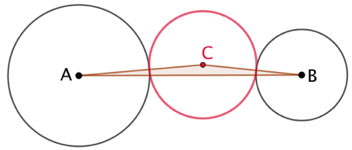
Conditions d’existence de ces cercles :
 |
 |
| Il ne faut pas que le cercle recherché puisse « passer entre les deux cercles » : |
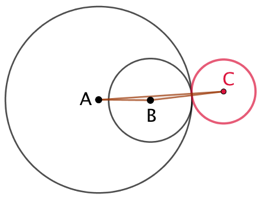
Il ne faut pas que le cercle de centre A « avale » le cercle de centre B, ou l’inverse : |
