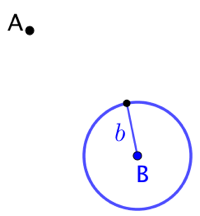
Cercle de rayon donné passant un point et tangent à un cercle

Soient un point A et un cercle de centre B et de rayon b. On cherche à tracer le cercle de rayon c passant par A et tangent au cercle de centre B.

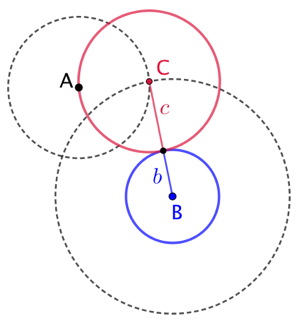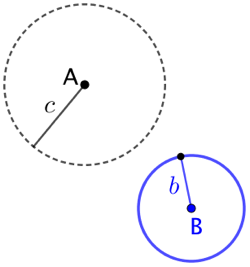
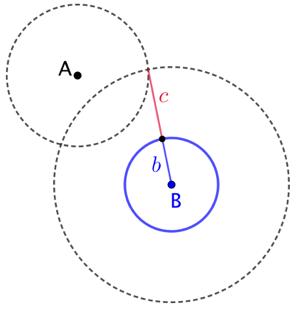
Soit C le centre du cercle recherché. Puisque A doit appartenir à un cercle de rayon c et de centre C, alors AC = c. Donc on trace un cercle de centre A et de rayon c.

Puisque le cercle de centre C et de rayon c doit être tangent au cercle de centre B et de rayon b, alors BC = b + c. Donc on trace un cercle de centre B et de rayon b + c.

Les deux intersection des deux cercles donnent les deux positions possibles pour le point C.

Les conditions d’existence du cercle : Cette construction est équivalente à celle d’un triangle ABC dont les longueurs des côtés sont : AB, AC = c et BC = b + c. Il faut donc que l’inégalité triangulaire soit respectée :

  • la distance AB doit être inférieure à b + 2c.
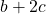  • A doit être situé à l’extérieur du cercle de centre B sinon BC > AB + AC.

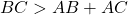En résumé : A doit être situé strictement à l’intérieur d’une couronne circulaire de petit rayon b et de grand rayon b + c.

 

Print Friendly, PDF & Email