Centre d’un cercle (version 3)

Étant donné un arc de cercle, on recherche le centre du cercle auquel appartient cet arc ainsi :

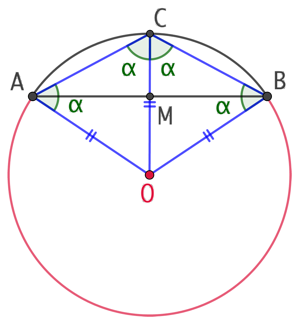
Soit M le centre du segment [AB] et C le point d’intersection de l’arc de cercle avec la perpendiculaire à (AB) passant par M.

1^er cas : L’arc de cercle est plus court qu’un demi cercle

On place sur la droite (MC) le point O tel que . Alors le triangle AOC est isocèle en O. La symétrie de la figure nous assure que le triangle COB est isocèle en O.

Puisque , A, B et C appartiennent au cercle de centre O.

Voir : la copie d’un angle 

2^ème cas : L’arc de cercle est un demi cercle

C’est un cas particulier du cas n°1 où les points O et M sont confondus.

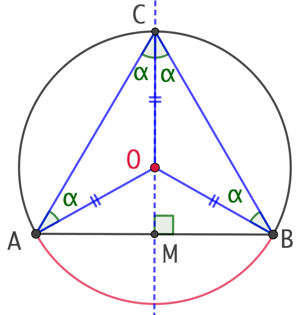3^ème cas : L’arc de cercle est plus grand qu’un demi cercle

La construction et le raisonnement sont semblables.

Remarque : Il s’agit de la proposition III.25 des Éléments d’Euclide.