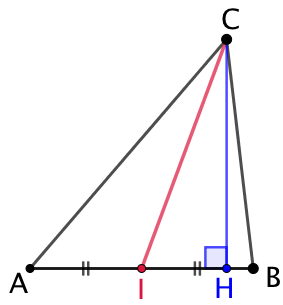
 Soit ABC un triangle, I le pied de la médiane issue de C et H le pied de la hauteur issue de C. On démontre l’égalité suivante :
Soit ABC un triangle, I le pied de la médiane issue de C et H le pied de la hauteur issue de C. On démontre l’égalité suivante : ![]() .
.
Explications :
Théorème de Pythagore appliqué à CAH, CHB et CIH :
![]()
Alors : ![]()
![]()
![]()
Donc ![]()
Ce qui est affirmé sans preuve peut être nié sans preuve (Euclide). Le but ultime n'est rien, le mouvement est tout (Eduard Bernstein)

 Soit ABC un triangle, I le pied de la médiane issue de C et H le pied de la hauteur issue de C. On démontre l’égalité suivante :
Soit ABC un triangle, I le pied de la médiane issue de C et H le pied de la hauteur issue de C. On démontre l’égalité suivante : ![]() .
.
Explications :
Théorème de Pythagore appliqué à CAH, CHB et CIH :
![]()
Alors : ![]()
![]()
![]()
Donc ![]()