I – Division euclidienne
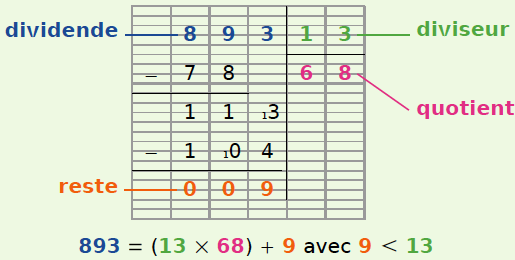 Exemple : On pose et on calcule la division de 893 par 13.
Exemple : On pose et on calcule la division de 893 par 13.
Exemple : Un fleuriste a reçu 260 roses. Il prépare des corbeilles de 12 roses chacune. Combien de corbeilles peut-il préparer ?
On cherche combien de fois il y a 12 dans 260 : 260 = (12 × 21) + 8 avec 8 < 12.
Il pourra donc préparer 21 corbeilles de 12 roses mais il lui restera 8 roses.
II – Divisibilité
1) Multiples et diviseurs d’un nombre entier
- Après avoir effectué la division euclidienne de 91 par 7, on obtient 91 = 7 × 13.
- Le reste étant nul, 91 est un multiple de 7 (et de 13 aussi !).
- On dit également que 91 est divisible par 7 ou que 7 est un diviseur de 91 ou que 7 divise 91.
2) Critères de divisibilité
- Un nombre entier est divisible par 2 si son chiffre des unités est 0, 2, 4, 6 ou 8.
- Un nombre entier est divisible par 3 si la somme de ses chiffres est un multiple de 3.
- Un nombre entier est divisible par 5 si son chiffre des unités est 0 ou 5.
- Un nombre entier est divisible par 9 si la somme de ses chiffres est un multiple de 9.
Exemple : On considère le nombre 23 928. Est-il divisible par 2, 5, 3 et 9 ?
- Son chiffre des unités est 8 donc 23 928 est divisible par 2.
- Son chiffre des unités n’est ni 0 ni 5 donc 23 928 n’est pas divisible par 5.
- La somme de ses chiffres : 2 + 3 + 9 + 2 + 8 soit 24 est un multiple de 3 donc 23 928 est divisible par 3.
- La somme de ses chiffres : 2 + 3 + 9 + 2 + 8 soit 24 n’est pas un multiple de 9 donc 23 928 n’est pas divisible par 9.
III – Nombres premiers
Autrement dit un nombre premier ne possède que deux diviseurs.
Exemples : 2 ; 3 ; 5 ; 7 ; 11 ; 13 ; 17 ; 19 ; 23 et 29 sont les nombres premiers inférieurs à 30.
Attention : 1 n’est pas un nombre premier car il ne possède qu’un seul diviseur : lui-même.
Décomposer un entier naturel en facteurs premiers, c’est trouver tous ses diviseurs qui sont des nombres premiers tels que le produit de tous ces nombres premier soit égal à l’entier naturel de départ.
Exemple : Décomposons l’entier naturel 60
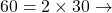 2
2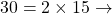 2
2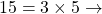 3
3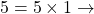 5
5
La décomposition est achevée lorsque le dernier quotient trouvé est 1.
Donc ![]() .
.
EXERCICES
Exercice n°1 : Dans la division euclidienne par 7, le reste est 3 et le quotient est 15. Quel est ce nombre ?
Exercice n°2 : Compléter
Exercice n°3 : 5346 est-il un multiple de 9 ?
Exercice n°4 :
- Vérifier que :
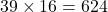
- En déduire, sans poser d’opération, que 4 et 13 sont des diviseurs de 624.
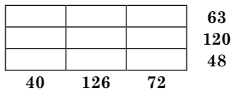 Exercice n°5 : Placer les nombres de 1 à 9. En bout de ligne ou de colonne figure le produit des 3 nombres de la ligne ou de la colonne.
Exercice n°5 : Placer les nombres de 1 à 9. En bout de ligne ou de colonne figure le produit des 3 nombres de la ligne ou de la colonne.
Exercice n°6 : Trouver la valeur du chiffre manquant représenté́ par un trèfle dans le nombre entier ![]() pour qu’il soit divisible par 3 et 5.
pour qu’il soit divisible par 3 et 5.
Exercice n°7 :
- Calculer :
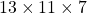
- Montrer que 325 325 est un multiple de 325 ; En déduire que 13, 77 et 143 sont des diviseurs de 325 325.
Exercice n°8 : Décomposer les nombres suivants en produits de facteurs premiers : ![]() .
.
Exercice n°9 : Quel sera le jour de la semaine dans 100 jours ? Dans 1000 jours ?
Exercice n°10 : Je suis un nombre divisible par 3, 5 et 9. Je suis compris entre 300 et 350. Qui suis-je ?
Exercice n°11 : Je suis un nombre divisible par 3, 5 et 2. Je suis compris entre 365 et 440, et la somme de mes chiffres est inférieure à 10. Qui suis-je ?
Exercice n°12 : Si on calcule le produit de ![]() , quels sont les chiffres des centaines, des dizaines et des unités de ce produit ?
, quels sont les chiffres des centaines, des dizaines et des unités de ce produit ?
Exercice n°13 : Parmi les nombres suivants, trouver 4 nombres dont la somme vaut 80 :
![]()
Exercice n°14 : Trouver 3 nombres dont le produit vaut 504. Même question avec ![]() .
.
