I – Diviseurs et multiples
On dit aussi que ![]() est divisible par
est divisible par ![]() ou que
ou que ![]() est un multiple de
est un multiple de ![]() (ou encore que
(ou encore que ![]() divise
divise ![]() ).
).
Exemple : ![]() est un multiple de
est un multiple de ![]() car
car ![]() .
. ![]() est aussi un multiple de
est aussi un multiple de ![]() .
.
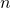 est pair si et seulement s’il existe
est pair si et seulement s’il existe 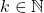 tel que
tel que 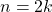 .
.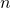 est pair si et seulement s’il existe
est pair si et seulement s’il existe 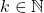 tel que
tel que 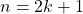 .
.
Démonstration : Soient ![]() et
et ![]() deux multiples de
deux multiples de ![]() .
.
Alors il existe deux entiers ![]() et
et ![]() tels que :
tels que : ![]() et
et ![]() .
.
![]() . Ce qui démontre que
. Ce qui démontre que ![]() et un multiple de
et un multiple de ![]() .
.
On démontre de façon similaire que ![]() est aussi un multiple de
est aussi un multiple de ![]() .
.
- Le carré d’un nombre pair est pair.
- Le carré d’un nombre impair est impair.
Démonstration : Soit ![]() et supposons que
et supposons que ![]() est impair.
est impair.
Alors il existe ![]() tel que
tel que ![]() .
.
![]() . Donc
. Donc ![]() est la somme d’un multiple de 2 et 1. Cela démontre que
est la somme d’un multiple de 2 et 1. Cela démontre que ![]() est impair.
est impair.
On démontre de façon similaire que le carré d’un nombre pair est pair.
II – Nombres premiers
Exemples : 2 ; 3 ; 5 ; 7 ; 11 ; 13 ; 17 ; 19 sont les 8 nombres premiers plus petits que 20.
Attention : 1 n’est pas un nombre premier.
Exemple : 14 et 15 sont premiers entre eux. Car :
- les diviseurs de 14 sont : 1 ; 2 ; 7 et 14.
- les diviseurs de 15 sont : 1 ; 3 ; 5, et 15.
Exemple : Décomposons 360
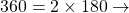 2
2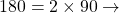 2
2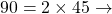 2
2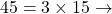 3
3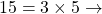 3
3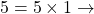 5
5
Donc ![]()
Simplifier une fraction c’est trouver une fraction irréductible qui lui soit égale. La méthode consiste à déterminer les décompositions en facteurs premiers du numérateur et du dénominateur.
Exemple : Simplifions ![]()
On sait déjà que ![]()
![]()
![]()
III – 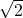 n’est pas un nombre rationnel
n’est pas un nombre rationnel
L’arithmétique nous permet de démontrer que la racine de 2 ne peut être un nombre rationnel. Pour cela utilise un raisonnement par l’absurde qui consiste à supposer le contraire de ce qu’on veut démontrer pour arriver à une contradiction qui permet alors d’affirmer que notre supposition était fausse et que son contraire est par conséquent vrai.
Supposons donc que ![]() est un nombre rationnel. Alors il existe
est un nombre rationnel. Alors il existe ![]() et
et ![]() , tels que
, tels que ![]() . On suppose de plus que la fraction
. On suppose de plus que la fraction ![]() est irrationnelle, donc que
est irrationnelle, donc que ![]() et
et ![]() sont premiers entre eux.
sont premiers entre eux.
Alors ![]() , soit
, soit ![]() .
.
Donc ![]() , ce qui implique que
, ce qui implique que ![]() est un nombre pair, donc que
est un nombre pair, donc que ![]() est un nombre pair. Si
est un nombre pair. Si ![]() était impair, alors une propriété précédente nous apprend que
était impair, alors une propriété précédente nous apprend que ![]() serait aussi impair, or nous savons que
serait aussi impair, or nous savons que ![]() est pair.
est pair.
Si ![]() est pair, il existe
est pair, il existe ![]() , tel que
, tel que ![]() , ce qui donne
, ce qui donne ![]() .
.
On sait ![]() donc
donc ![]() , ce qui donne
, ce qui donne ![]() . Ce qui implique que
. Ce qui implique que ![]() est pair, donc que
est pair, donc que ![]() est pair.
est pair.
Nous venons d’arriver à la conclusion que ![]() et
et ![]() sont pairs, donc divisibles par 2. Donc ils ne sont pas premiers entre eux. Or nous avions supposés qu’ils étaient premiers entre eux !
sont pairs, donc divisibles par 2. Donc ils ne sont pas premiers entre eux. Or nous avions supposés qu’ils étaient premiers entre eux !
Nous aboutissons à une contradiction dans notre raisonnement. Notre supposition était fausse et le nombre ![]() est irrationnel.
est irrationnel.
