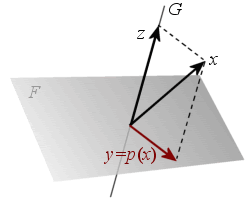
![]()
La composition de deux applications linéaires est une application linéaire.
Soient ![]() et
et ![]() :
:
![]()
Soit ![]() ∶
∶
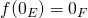 et
et 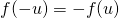
- Si
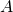 est un SEV de
est un SEV de 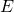 alors
alors 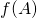 est un SEV de
est un SEV de 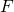 . Si
. Si 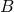 est un SEV de
est un SEV de 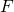 alors
alors 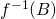 est un SEV de
est un SEV de 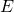 .
. - Im
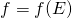 et Ker
et Ker 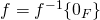
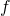 est injective
est injective  Ker
Ker 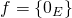
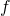 est surjective
est surjective  Im
Im 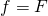
- L’image d’une famille liée est une famille liée. L’image réciproque d’une famille libre est une famille libre.
- L’image d’une famille libre par une application linéaire injective est libre.
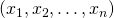 est une famille libre et si
est une famille libre et si 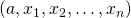 est une famille liée, alors
est une famille liée, alors  est égal à une unique combinaison linéaire de
est égal à une unique combinaison linéaire de 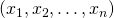 .
.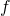 est caractérisée par ses restrictions à deux SEV supplémentaires dans E.
est caractérisée par ses restrictions à deux SEV supplémentaires dans E.- Im
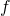 est isomorphe à tout SEV supplémentaire de Ker
est isomorphe à tout SEV supplémentaire de Ker 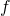 dans
dans 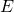 .
.
groupe linéaire de E : ![]() , l’ensemble des automorphismes sur
, l’ensemble des automorphismes sur ![]() , est stable par la composition.
, est stable par la composition.
Homothéties :
Ce sont des endomorphismes. ![]() et
et ![]() si
si ![]() .
.
Les homothéties commutent avec tous les endomorphismes.
![]()
Projecteurs
![]() projecteur sur
projecteur sur ![]() parallèlement à
parallèlement à ![]()
![]()
Propriétés :
Si ![]() est un projecteur sur
est un projecteur sur ![]() parallèlement à
parallèlement à ![]() alors
alors ![]() est un projecteur sur
est un projecteur sur ![]() parallèlement à
parallèlement à ![]() .
.
![]()
Les projecteurs sont exactement les endomorphismes idempotents.
Symétries
![]() symétrie par rapport à
symétrie par rapport à ![]() parallèlement à
parallèlement à ![]()
![]()
Propriétés :
![]()
![]() est une symétrie si et seulement si
est une symétrie si et seulement si ![]() est un projecteur.
est un projecteur.
![]()
Les symétries sont exactement les endomorphismes involutifs.
Endomorphismes nilpotents
Soit ![]() . L’indice de u est le plus petit entier naturel k tel que
. L’indice de u est le plus petit entier naturel k tel que ![]() et
et ![]() .
.
Propriétés dans un espace vectoriel de dimension finie ![]() :
:
Soit un endomorphisme nilpotent ![]() d’indice
d’indice ![]() .
.
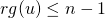
- Si
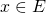 vérifie
vérifie 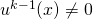 alors la famille
alors la famille 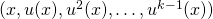 est libre.
est libre. 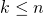
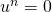 . C’est une condition nécessaire et suffisante pour qu’un endomorphisme soit nilpotent.
. C’est une condition nécessaire et suffisante pour qu’un endomorphisme soit nilpotent.
Dans un espace vectoriel de dimension finie
Une application linéaire est déterminée de manière unique par l’image d’une base : soit ![]() une base de
une base de ![]() .
. ![]() telle que
telle que ![]()
Propriétés :
- Im
 = Vect
= Vect  .
. 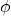 est injective si et seulement si
est injective si et seulement si 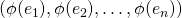 est une famille libre de F.
est une famille libre de F.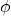 est surjective si et seulement si
est surjective si et seulement si 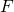 = Vect
= Vect 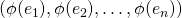 .
. est un isomorphisme si et seulement si
est un isomorphisme si et seulement si 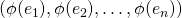 est une base de
est une base de 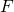 .
.
- Deux espaces vectoriels de même dimension finie sont isomorphes.
- Donc tout espace vectoriel de dimension
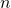 est isomorphe à
est isomorphe à 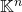 .
. - Si dim
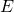 = dim
= dim  F alors :
F alors : 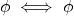 injective
injective 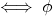 surjective
surjective 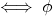 bijective
bijective
Rang d’une application linéaire
![]()
Propriétés :
![]()
Le rang d’une application linéaire est invariant par composition par un isomorphisme.
Théorème du rang : dim Ker ![]() + dim Im
+ dim Im ![]() = dim E = dim Ker
= dim E = dim Ker ![]() + rg
+ rg ![]()
![]() ∶
∶ ![]() = Ker
= Ker ![]() Im
Im ![]() ker
ker ![]() + Im
+ Im ![]() est une somme directe.
est une somme directe.
Équations linéaires : 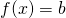
- Si
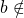 Im
Im 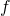 alors pas de solution
alors pas de solution - Soit
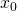 une solution particulière. L’ensemble des solutions est
une solution particulière. L’ensemble des solutions est 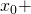 Ker
Ker 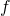 .
.