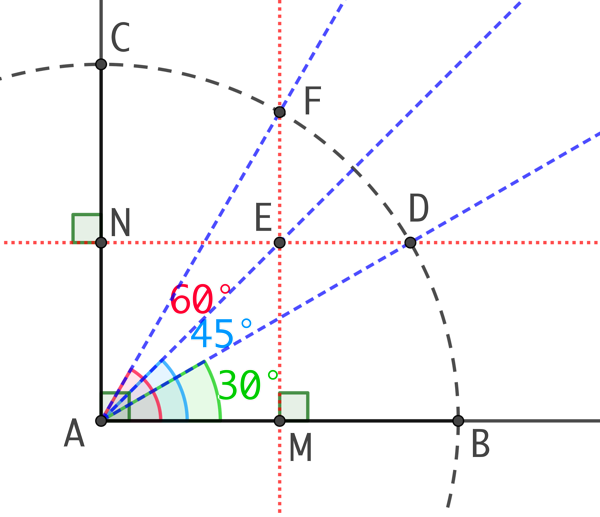
On peut aussi construire des angles de 30°, 45° et 60° ainsi :
- On trace une demi-droite [AB) et la demi-droite perpendiculaire à [AB) passant par A.
- On trace un cercle de centre A et de rayon AB. Ce cercle coupe la perpendiculaire à [AB) au point C.
- On place M milieu du segment [AB] et on trace la perpendiculaire à [AB) passant par M. Elle coupe le cercle au point F. L’angle
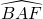 mesure 60°.
mesure 60°. - On place N milieu du segment [AC] et on trace la perpendiculaire à [AC) passant par N. Elle coupe le cercle au point D. L’angle
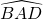 mesure 30°.
mesure 30°. - On place le point E intersection des droites (MF) et (ND). L’angle
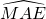 mesure 45°.
mesure 45°.
Explications :
On fait appel à la trigonométrie. N est le milieu de [AC] donc ![]() . Or
. Or ![]() , ce qui correspond au sinus d’un angle de 30°.
, ce qui correspond au sinus d’un angle de 30°.
M est le milieu de [AB] donc ![]() . Or
. Or ![]() , ce qui correspond au cosinus d’un angle de 60°.
, ce qui correspond au cosinus d’un angle de 60°.
Par construction le quadrilatère AMEN est un carré. Donc la demi-droite [AE) porte la diagonale de ce carré et par conséquent ![]()
![]() .
.
