 L’aire du triangle ABE est égale au produit de la longueur de l’un de ses côtés multipliée par la longueur de la hauteur perpendiculaire à ce côté, le tout divisé par 2.
L’aire du triangle ABE est égale au produit de la longueur de l’un de ses côtés multipliée par la longueur de la hauteur perpendiculaire à ce côté, le tout divisé par 2.
Explications :
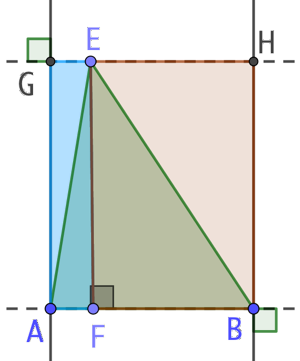
On trace la hauteur de ABE issue de E. Elle coupe la droite (AB) en F. L’aire du triangle ABE est la somme des aires des triangles rectangles EFA et EFB.
On trace la parallèle à (AB) qui passe par E.
On trace les perpendiculaires à (AB) qui passent par A et par B. Elles coupent la parallèle à (AB) en G et en H.
Par construction le quadrilatère EFAG est un rectangle dont l’une de ses diagonales est (AE). On sait que l’aire de EFAG est le double de celle du triangle EFA.
Par un raisonnement identique on montre que le rectangle EFBH a une aire double de celle du triangle EFB.
La somme de l’aire de EFAG et de l’aire de EFBH est égale à l’aire de ABHG, soit ![]() ou
ou ![]() puisque
puisque ![]() . Donc l’aire de ABE vaut
. Donc l’aire de ABE vaut ![]() .
.
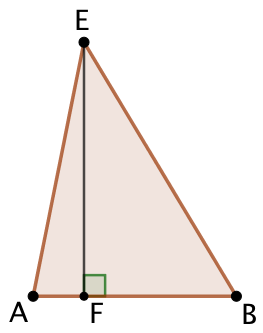
Autre approche :
 |
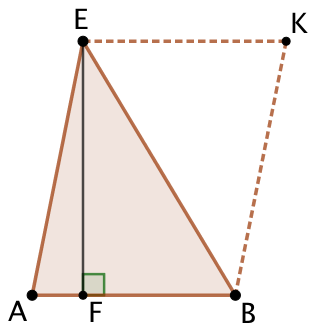 |
On complète le triangle de gauche en construisant la parallèle à (AB) passant par E et la parallèle à (AE) passant par B. Ces deux droites se coupent en K. ABKE est un parallélogramme dont l’aire est le double de celle de ABE. L’aire du parallélogramme est AB x EF.
Ce qui justifie la formule de l’aire du triangle : ![]()
