Aire du poisson

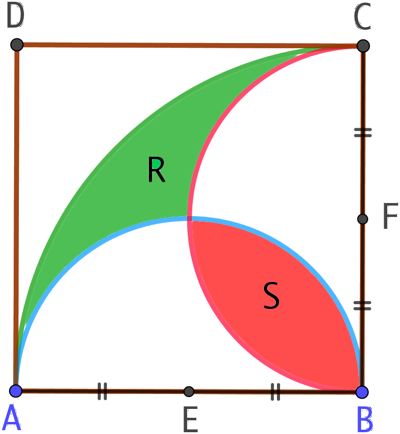
Etant donnés :

  • un carré ABCD dont chaque côté mesure a;
  • un quart de cercle de rayon a et de centre B;
  • deux demi-cercles de rayon 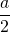\dfrac{a}{2} et de centre E et F.

On démontre que l’aire R est égale à l’aire S.

Explications :

L’aire R s’obtient en partant de l’aire du quart de disque de centre B et de rayon a, et en lui retirant les deux demi-disques de rayon \dfrac{a}{2} et de centre E et F. Mais en procédant ainsi on retire deux fois l’aire S, donc pour obtenir l’aire R, il faut ajouter une fois l’aire S.

L’aide du quart de disque est  : \dfrac{\pi a^2}{4}.

Calculer l’aire de deux demi-disques de rayon \dfrac{a}{2} revient à calculer l’aire d’un disque entier de même rayon : \pi \left ( \dfrac{a}{2} \right ) ^2 = \dfrac{\pi a^2}{4}.

Donc R = \dfrac{\pi a^2}{4} - \dfrac{\pi a^2}{4} + S. Donc R = S.

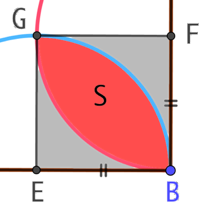Calcul de l’aire S :

Soit A_C l’aire du carré EBFG et A_G l’aire de chaque zone grise (dessin de droite). Alors S = A_C - 2 A_G.

Soit A_Q l’aire du quart du disque de centre F (ou E) et de rayon \dfrac{a}{2}. Alors A_G = A_C - A_Q.

Donc S = A_C - 2 (A_C - A_Q) = 2A_Q - A_C.

A_C = \left ( \dfrac{a}{2} \right ) ^2 et A_Q = \dfrac{1}{4} \pi \left ( \dfrac{a}{2} \right ) ^2

Donc S = \dfrac{\pi}{2} \left ( \dfrac{a}{2} \right ) ^2 - \left ( \dfrac{a}{2} \right ) ^2 = \left ( \dfrac{a}{2} \right ) ^2 \left ( \dfrac{\pi}{2} - 1 \right ) = \dfrac{a^2}{8} (\pi - 2).

Print Friendly, PDF & Email