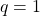I – Définition et mode de génération
Exemple : ![]()
Exemple : La suite ![]() définie sur
définie sur ![]() par
par ![]() est définie explicitement. En donnant à
est définie explicitement. En donnant à ![]() différentes valeurs, on obtient par le calcul
différentes valeurs, on obtient par le calcul ![]()
Exemple : La suite ![]() définie sur
définie sur ![]() et
et ![]() par
par ![]() .
. ![]() est définie par récurrence. Ainsi pour calculer
est définie par récurrence. Ainsi pour calculer ![]() , il faut calculer
, il faut calculer ![]() d’abord :
d’abord : ![]() .
.
II – Représentation graphique d’une suite
Une suite ![]() peut être représentée soit en plaçant les réels
peut être représentée soit en plaçant les réels ![]() sur une droite graduée, soit en plaçant les points
sur une droite graduée, soit en plaçant les points ![]() dans un repère.
dans un repère.
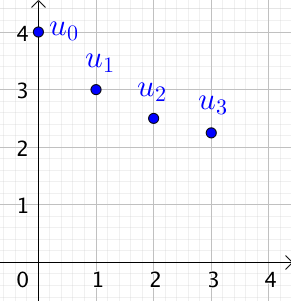
Exemple : la suite ![]() définie précédemment se représente des deux façons suivantes :
définie précédemment se représente des deux façons suivantes :
 |
 |
III – Sens de variation
Une suite ![]() est croissante à partir du rang
est croissante à partir du rang ![]() si et seulement si pour tout entier naturel
si et seulement si pour tout entier naturel ![]() .
.
Une suite ![]() est décroissante à partir du rang
est décroissante à partir du rang ![]() si et seulement si pour tout entier naturel
si et seulement si pour tout entier naturel ![]() .
.
Une suite croissante ou décroissante est dite monotone.
Exemple : La suite ![]() définie précédemment est décroissante.
définie précédemment est décroissante.
IV – Suites arithmétiques
Exemple : La suite ![]() définit par
définit par ![]() et
et ![]() est la suite arithmétique de premier terme
est la suite arithmétique de premier terme ![]() et de raison
et de raison ![]() .
.
Démonstration : Supposons que ![]() .
.
![]() donc
donc ![]()
![]() donc
donc ![]() et ainsi de suite jusqu’à arriver à
et ainsi de suite jusqu’à arriver à ![]() .
.
Pour passer de ![]() à
à ![]() , il faut ajouter
, il faut ajouter ![]() fois la raison à
fois la raison à ![]() .
.
Supposons que ![]() . Alors en utilisant la première partie de la démonstration, on peut écrire que
. Alors en utilisant la première partie de la démonstration, on peut écrire que ![]() donc
donc ![]() .
.
Démonstration : Posons ![]() . On peut aussi écrire
. On peut aussi écrire ![]() .
.
Alors ![]()
Soit ![]() .
.
Conclusion : ![]() .
.
- croissante si
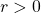
- décroissante si
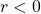
- constante si
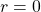
Démonstration : Soit suite ![]() une suite arithmétique de raison
une suite arithmétique de raison ![]() . Alors
. Alors ![]() . Donc
. Donc ![]()
Si ![]() alors
alors ![]() donc
donc ![]() . Ce qui prouve que la suite est croissante.
. Ce qui prouve que la suite est croissante.
Si ![]() alors
alors ![]() donc
donc ![]() . Ce qui prouve que la suite est décroissante.
. Ce qui prouve que la suite est décroissante.
Si ![]() alors
alors ![]() donc
donc ![]() . Ce qui prouve que la suite est constante.
. Ce qui prouve que la suite est constante.
V – Suites géométriques
Exemple : La suite géométrique ![]() est définit par
est définit par ![]() et raison 2.
et raison 2. ![]()
- croissante si
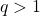
- décroissante si
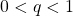
- constante si