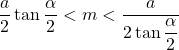On veut construire un triangle ABC pour lequel on donne la longueur 
d’un côté [BC], la longueur 
de la médiane issue du sommet A et la mesure 
de l’angle 
.
 |
 |
 |
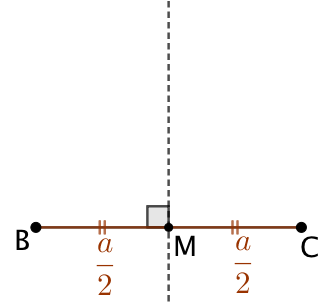
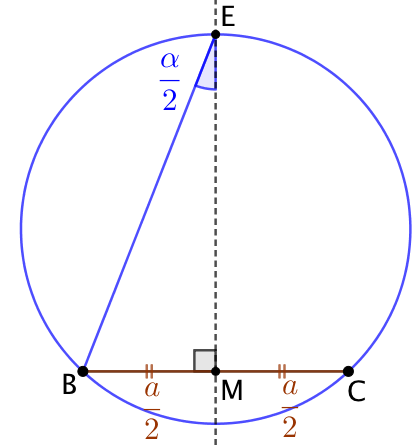
| On trace la médiatrice de [BC]. | Le point E de la médiatrice est tel qu’il voit [BC] sous un angle . On trace le cercle passant par B, C et E. |
On trace le cercle de centre M et de rayon . Les cercles se coupent en deux points qui sont les deux possibles pour le point A. |
Explications :
Dans le triangle rectangle BME, 
donc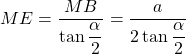 
Dans le cercle unique passant par B, E et C, les angles 
et interceptent le même arc de cercle BC, donc ils ont la même mesure.
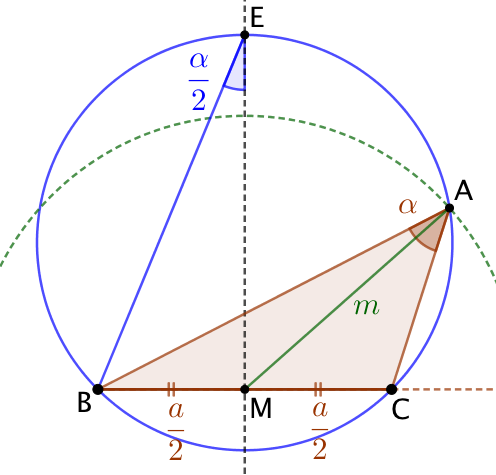
Conditions d’existence du triangle ABC :
Soit F l’autre point d’intersection de la médiatrice de [BC] et du cercle passant par B, C et E. Les triangles BME et FMB sont sembles. Donc 
. Ce qui donne : 
ABC existe à condition que : 
, soit : 
