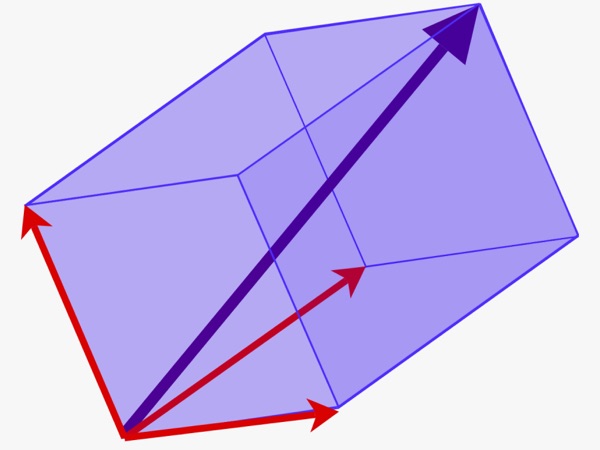
![]() muni d’une loi de composition interne + et d’une loi de composition externe * à opérateurs dans
muni d’une loi de composition interne + et d’une loi de composition externe * à opérateurs dans ![]() .
.
![]() est un
est un ![]() -espace vectoriel si et seulement si :
-espace vectoriel si et seulement si :
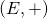 est un groupe commutatif
est un groupe commutatif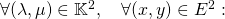
Algèbre
![]() est une
est une ![]() -algèbre si et seulement si
-algèbre si et seulement si
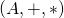 est un
est un 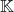 -espace vectoriel
-espace vectoriel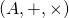 est un anneau
est un anneau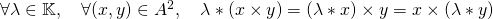
SOUS-ESPACES VECTORIELS (SEV)
![]() est un sous-espace vectoriel de
est un sous-espace vectoriel de ![]() si et seulement si :
si et seulement si :
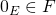
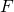 stable par + et par * ou par combinaison linéaire
stable par + et par * ou par combinaison linéaire
L’intersection de deux SEV de ![]() est un SEV de
est un SEV de ![]() .
.
SEV engendré : Soient ![]() ,
,
![Rendered by QuickLaTeX.com \[ \text{Vect} (x_1,x_2, \dots ,x_p ) = \left \{ \sum_{k=1}^p \lambda_k x_k, (\lambda_1,\lambda_2, \dots ,\lambda_p ) \in \mathbb{K}^p} \right \} \]](http://www.rozenblum.com/wp-content/ql-cache/quicklatex.com-d3bbfe3bf418d76030f92c9489988458_l3.png)
est le SEV engendré par la famille finie des vecteurs ![]() .
.
Somme de SEV
![]()
![]() est le plus petit SEV de
est le plus petit SEV de ![]() contenant
contenant ![]() et
et ![]() :
: ![]() .
.
Somme directe de SEV
![]()
![]()
![]() et
et ![]() sont deux SEV supplémentaires dans
sont deux SEV supplémentaires dans ![]() si et seulement si
si et seulement si ![]() .
.
Deux SEV supplémentaires d’un même troisième SEV sont isomorphes.
Familles libres, liées, génératrices, bases
![]()
![]()
![]()
![]()
ESPACES VECTORIELS DE DIMENSION FINIE
On suppose que ![]() est un espace vectoriel de dimension finie
est un espace vectoriel de dimension finie ![]() .
.
Théorème de la base incomplète : Si ![]() est une famille libre de
est une famille libre de ![]() , alors il existe des vecteurs
, alors il existe des vecteurs ![]() (que l’on peut prendre dans une famille génératrice quelconque fixée à l’avance) tels que
(que l’on peut prendre dans une famille génératrice quelconque fixée à l’avance) tels que ![]() soit une base de
soit une base de ![]() .
.
Si ![]() est un SEV de
est un SEV de ![]() , alors
, alors ![]() admet un SEV supplémentaire
admet un SEV supplémentaire ![]() dans
dans ![]() et dim
et dim ![]() = dim
= dim ![]() – dim
– dim ![]() .
.
Si ![]() et
et ![]() sont deux SEV de
sont deux SEV de ![]() , alors dim
, alors dim ![]() = dim
= dim ![]() + dim
+ dim ![]() – dim
– dim ![]() .
.
Rang d’une famille
![]()
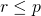 et
et 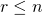
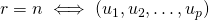 est une famille génératrice de
est une famille génératrice de 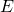
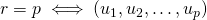 est une famille libre de
est une famille libre de 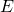
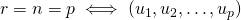 est une base de
est une base de 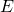
HYPERPLANS ET ESPACE DUAL
Un hyperplan est un SEV qui admet une droite vectorielle pour supplémentaire.
![]() est un hyperplan de
est un hyperplan de ![]() si et seulement si
si et seulement si ![]() .
.
![]() est un hyperplan de
est un hyperplan de ![]() si et seulement si il existe une forme linéaire
si et seulement si il existe une forme linéaire ![]() telle que Ker
telle que Ker ![]() . Les hyperplans sont exactement les noyaux de formes linéaires non nulles définies sur
. Les hyperplans sont exactement les noyaux de formes linéaires non nulles définies sur ![]() .
.
Espace dual
L’espace dual de ![]() est noté
est noté ![]() . C’est le
. C’est le ![]() -espace vectoriel des formes linéaires sur
-espace vectoriel des formes linéaires sur ![]() .
.
Soit ![]() une base de
une base de ![]() .
.
La base duale de ![]() associée à
associée à ![]() est
est ![]() définie par
définie par ![]()
![Rendered by QuickLaTeX.com \[ \text{Soit } f \in E^* \quad \text{Alors } \quad f = \sum_{i=1}^n f(e_i)e_i^*$ \]](http://www.rozenblum.com/wp-content/ql-cache/quicklatex.com-d6d13745d273c218cc55afd368b76179_l3.png)