 La bissectrice d’un angle est le lieu géométrique des points équidistants des deux côtés de l’angle.
La bissectrice d’un angle est le lieu géométrique des points équidistants des deux côtés de l’angle.
Explications :
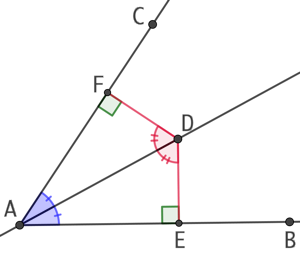
Soit D un point de la bissectrice de l’angle ![]() . Soient E et F les projetés orthogonaux de D sur les deux côtés de l’angle
. Soient E et F les projetés orthogonaux de D sur les deux côtés de l’angle ![]() .
.
On a ![]() et
et ![]() donc les triangles FAD et DAE sont semblables. Comme ils possèdent un côté commun [AD], ils sont isométriques. Par conséquent
donc les triangles FAD et DAE sont semblables. Comme ils possèdent un côté commun [AD], ils sont isométriques. Par conséquent ![]() , c’est-a-dire que D est équidistant des deux côtés de l’angle
, c’est-a-dire que D est équidistant des deux côtés de l’angle ![]() .
.
Réciproque : Si un point D est équidistant des deux côtés de l’angle ![]() alors il appartient à la bissectrice de cet angle.
alors il appartient à la bissectrice de cet angle.
On reprend les mêmes notations. On sait que ![]() et que les angles
et que les angles ![]() et
et ![]() sont droits. En utilisant le théorème de Pythagore sur les triangles FAD et DAE, on démontre que
sont droits. En utilisant le théorème de Pythagore sur les triangles FAD et DAE, on démontre que ![]() . Ces deux triangles sont alors isométriques, ce qui permet d’affirmer que
. Ces deux triangles sont alors isométriques, ce qui permet d’affirmer que ![]() , c’est à dire que la droite (AD) est la bissectrice intérieure de
, c’est à dire que la droite (AD) est la bissectrice intérieure de ![]() .
.
