 Le nombre d’or,
Le nombre d’or, ![]() , est le coefficient de proportionnalité entre deux grandeurs
, est le coefficient de proportionnalité entre deux grandeurs ![]() et
et ![]() choisies de la manière suivante :
choisies de la manière suivante :
On montre que ![]() , soit environ 1,618.
, soit environ 1,618.
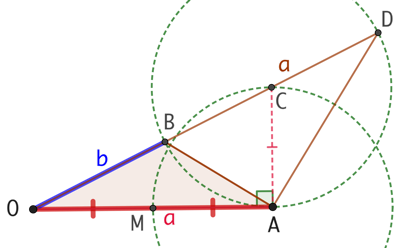
Construction :
- On trace un segment [OA] de longueur arbitraire
 ,
, - On place le milieu M de [OA],
- On trace la perpendiculaire à (OA) passant par A,
- On trace le cercle de centre A et de rayon AM, soit
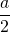 . Il coupe la perpendiculaire au point C,
. Il coupe la perpendiculaire au point C, - On trace le cercle de centre C et passant par A,
- On trace la droite (OC). Elle coupe le cercle de centre C en B,
- La longueur du segment [OB] est
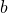 telle que
telle que 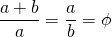 .
.
Explications :
D est le second point d’intersection entre (OB) et le cercle de centre C. ![]() . On démontre les triangles OAB et OAD sont semblables :
. On démontre les triangles OAB et OAD sont semblables :
Ils ont un angle en commun : ![]()
Les triangles OAC et BAD sont rectangles en A donc ![]() .
.
Le triangle CAD est isocèle en C donc ![]() .
.
Ainsi ![]() ce qui montre que les triangles OAB et OAD ont deux autres angles de même mesure. Ils sont donc semblables et les longueurs de leurs côtés sont proportionnels.
ce qui montre que les triangles OAB et OAD ont deux autres angles de même mesure. Ils sont donc semblables et les longueurs de leurs côtés sont proportionnels.
Donc ![]() .
.
Valeur du nombre d’or (méthode géométrique) :
Puisque la valeur de ![]() est arbitraire, on prend
est arbitraire, on prend ![]() .
.
Alors : ![]() .
.
Le théorème de Pythagore appliqué au triangle OAC donne ![]() .
.
Par ailleurs ![]() .
.
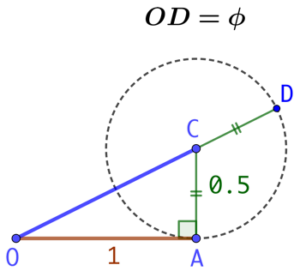 Cette méthode fournit le procédé de construction du nombre
Cette méthode fournit le procédé de construction du nombre ![]() :
:
- On trace un segment [OA] de longueur 1,
- On trace un segment [AC] de longueur 0,5 tel que (AC) et (AO) soient perpendiculaires,
- On trace le cercle de centre C et de rayon 0,5,
- On trace la droite (OC). Elle coupe le cercle au point D,
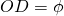 .
.
Valeur du nombre d’or (méthode algébrique) :
![]() donc
donc ![]() .
.
En multipliant par ![]() , on obtient
, on obtient ![]() .
.
Comme ![]() , l’équation à résoudre est
, l’équation à résoudre est ![]() ou
ou ![]() . La racine positive de cette équation est
. La racine positive de cette équation est ![]() .
.
