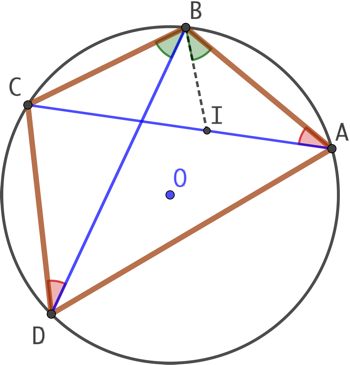
 Étant donné un quadrilatère ABCD inscrit dans un cercle de centre O, la somme des produits des côtés opposés est égale au produit des diagonales, soit :
Étant donné un quadrilatère ABCD inscrit dans un cercle de centre O, la somme des produits des côtés opposés est égale au produit des diagonales, soit : ![]() .
.
Explications :
On place le point I sur [AC] tel que ![]() . Voir Copie d’un angle.
. Voir Copie d’un angle.
Par ailleurs ![]() car ses angles interceptent le même arc de cercle BC.
car ses angles interceptent le même arc de cercle BC.
Par conséquent les triangles ABI et BCD sont semblables.
Donc ![]() , soit
, soit ![]() . (1)
. (1)
![]() donc
donc ![]() , soit
, soit ![]() .
.
Par ailleurs ![]() car ses angles interceptent le même arc de cercle AB.
car ses angles interceptent le même arc de cercle AB.
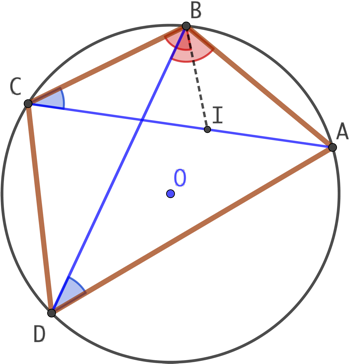 Par conséquent les triangles ABD et BCI sont semblables.
Par conséquent les triangles ABD et BCI sont semblables.
Donc ![]() , soit
, soit ![]() . (2)
. (2)
On additionne (1) et (2) : ![]() ,
,
soit ![]() ,
,
c’est à dire ![]() .
.
Claude Ptolémée (100 – 168) : astronome et mathématicien grec d’Égypte.
