Lorsqu’on étudie un certain caractère (couleur d’une voiture, taille d’un individu) sur une population donnée, on relève une valeur (rouge, 1 m 75) du caractère par individu.

L’ensemble des données obtenues (ou toutes les valeurs prises par le caractère) constitue les données brutes. Les données brutes comportent souvent des valeurs qui se répètent.

I – Série statistique

Définitions : série statistique

Lors d’un relevé de mesures effectué sur les individus d’une population, l’ensemble des données collectées constitue une série statistique.
Une série statistique à caractère quantitatif est dite ordonnée après que les valeurs collectées ont été rangées dans l’ordre croissant (ou décroissant).
L’étendue désigne l’écart entre la plus grande et la plus petite des valeurs
prises par le caractère.

Définition : tableau d'effectif

Le tableau d’effectif d’une série statistique à caractère quantitatif est constitué de deux lignes :

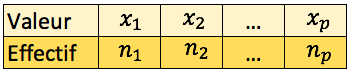
Première ligne : les différentes valeurs prises par le caractère étudié, rangé dans l’ordre croissant;
Deuxième ligne : les effectifs correspondants à chaque valeur de la première ligne

Exemple : On relève la pointure des pieds de 47 personnes. On présente cette série statistique sous la forme du tableau d’effectif ci-contre.

Ainsi le tableau nous apprend que 7 personnes de cette série ont une pointure de 40.

II – Fréquence et moyenne

Dans la suite du chapitre, on considère une série statistique à caractère quantitatif pour laquelle le caractère étudié possède $p$ valeurs différentes notées $x_1, x_2, \dots, x_p$ dont les effectifs correspondants sont $n_1, n_2, \dots, n_p$ , et dont l’effectif total est N.

Définition : fréquence d'apparition

La fréquence d’apparition de la valeur $x_k$ est $f_k = \dfrac{n_k}{N}$ .

Propriété

La somme des fréquences d’une série statistique est égale à 1.

Démonstration : $f_1 + f_2 + \dots + f_p = \dfrac{n_1}{N} + \dfrac{n_2}{N} + \dots + \dfrac{n_p}{N} = \dfrac{n_1 + n_2 + \dots + n_p}{N} = \dfrac{N}{N} = 1$ .

Exemple : À partir du tableau des pointures, on calcule les fréquences d’apparition, sachant que l’effectif total (le total de la seconde ligne) est de 47 individus. Les fréquences ont été calculées en valeur réelle et en pourcentage. On vérifie que le total des fréquences est égale à 1 ou à 100% si elles ont été calculées en pourcentage.

Définition : moyenne pondérée

La moyenne pondérée de la série statistique, notée $\overline{x}$ est donnée par la formule : $\dfrac{n_1 \times x_1 + n_2 \times x_2 + \dots + \n_p \times x_p}{N}$

On dit que l’on a pondéré chaque valeur $x_k$ par son effectif $n_k$ .

Propriété

Si on connait déjà les fréquences d’apparition, la moyenne pondérée s’obtient par la formule : $f_1 \times x_1 + f_2 \times x_2 + \dots + f_p \times x_p$ .

Démonstration : $\overline{x} = \dfrac{n_1 \times x_1 + n_2 \times x_2 + \dots + \n_p \times x_p}{N} = \dfrac{n_1 \times x_1}{N} + \dfrac{n_2 \times x_2}{N} + \dots + \dfrac{n_p \times x_p}{N}$

Donc $\overline{x} = \dfrac{n_1}{N} \times x_1 + \dfrac{n_2}{N} \times x_2 + \dots + \dfrac{n_p}{N} \times x_p = f_1 \times x_1 + f_2 \times x_2 + \dots + f_p \times x_p$ .

Exemple : La moyenne pondérée obtenue à partir du tableau des pointures, est d’environ 40,45.

III – Variance et écart-type

Lorsque l’on étudie les données fournies par une série statistique, on veut savoir si la majorité des individus étudiés sont proches de la moyenne ou si au contraire, il existe de fortes disparités entre les individus. Ces écarts à la moyenne se mesure avec l’écart-type de la série, c’est-à-dire la moyenne des écarts (des distances) à la moyenne de la série.

Définition : variance

La variance d’une série, notée $V$ , est la moyenne pondérée des carrés des écarts de chaque valeur à la moyenne $\overline{x}$ de la série.

Autrement dit : $V = \dfrac{ n_1 (x_1 - \overline{x})^2 + n_2 (x_2 - \overline{x})^2 + \dots + n_p (x_p - \overline{x})^2 }{N}$ .

Le mot « variance » fait référence à la variabilité du phénomène étudié.

Définition : écart-type

L’écart-type d’une série, noté $\sigma$ (lire sigma), est la racine carrée de la variance.

Si les valeurs de la série sont proches de la moyenne, alors la variance et l’écart-type sont faibles, et réciproquement. On dit que l’écart-type mesure la dispersion de la série autour de sa moyenne.

Remarque : Si les valeurs de la série s’expriment dans une certaine unité, l’écart-type s’exprime dans la même unité. C’est l’une des raisons qui explique qu’en statistique, c’est surtout l’écart-type qui est utilisé car plus intéressant que la variance.

Exemple : La variance et l’écart-type de la série statistique des pointures de pieds sont : $V = 4,12$ et $\sigma = 2,03$ .

IV – Médiane et quartiles

Définition : médiane

Dans une série statistique ordonnée : une médiane partage les valeurs prises par le caractère en deux groupes de même effectif.

La médiane d’une série statistique est la valeur telle qu’au moins la moitié des valeurs de la série soient inférieures ou égales à cette valeur et au moins la moitié des valeurs soient supérieures ou égales.

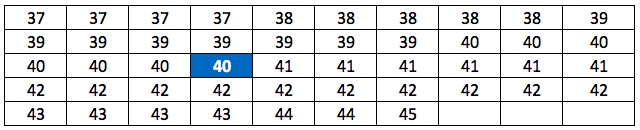Exemple : Reprenons nos pointures de chaussures. On trie les 47 individus par ordre croissant de pointure. Comme $47 = 2 \times 23 + 1$ , la 24^ème pointure, à savoir 40, représentée en bleu sur le tableau ci-contre, est la médiane de cette série statistique, puisqu’elle la divise en deux groupes de même effectif.

Remarque : Dans cette exemple, on observe que la médiane et la moyenne sont très proche : 40 et environ 40,45. Ce n’est pas toujours le cas. En général, la médiane est plus intéressante que la moyenne. À travers un exercice, on pourra se rendre compte que la médiane est moins sensible que la moyenne aux valeurs exceptionnelles contenues dans une série. La médiane est souvent plus précise que la moyenne pour décrire une série statistique.

Méthode : calcul de la médiane

Si l’effectif total est impair, une valeur restera entre les deux demi-groupes.
Cette valeur sera la médiane.
Si l’effectif total est pair, n’importe quelle valeur comprise entre la dernière valeur
du premier groupe et la première valeur du second groupe peut être considérée comme une médiane. Le plus souvent, la moyenne de ces deux valeurs est choisie comme médiane.

Exemple : Soit la série statistique suivante : $3 ; 5 ; 6 ; 11 ; 17 ; 22$ . L’effectif total est $6$ , donc pair. Le premier groupe de trois valeurs se termine par $6$ . Le deuxième groupe de trois valeurs débute par $11$ . On peut prendre comme médiane : $7, 8, 9$ ou $10$ , ou la moyenne de $6$ et de $11$ , soit $8,5$ .

Définitions : quartiles

Le premier quartile, souvent noté 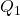$Q_1$ , d’une série statistique numérique est la plus petite valeur prise par le caractère telle qu’au moins 25% des valeurs lui soient inférieures ou égales.
Le troisième quartile, souvent noté 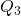$Q_3$ , d’une série statistique numérique est la plus petite valeur prise par le caractère telle qu’au moins 75% des valeurs lui soient inférieures ou égales.

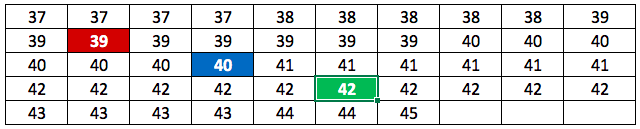Exemple : Reprenons nos pointures de chaussures. L’effectif total est de 47. 25% de 47 vaut 11,75. Donc “au moins 25%” correspond à la 12^ème valeur de la série ordonnée, soit $Q_1=39$ (en rouge dans le tableau).