SYSTÈMES LINÉAIRES
Pour déterminer les solutions d’un système linéaire (SL), on trouve une solution particulière que l’on ajoute à toutes les solutions du SL homogène SLH) correspondant.
Un SLH admet soit une solution unique soit une infinité de solution.
Un SL admet soit une solution unique soit une infinité de solution soit aucune solution.
Dans un SL ou une matrice, on appelle pivot le 1er coefficient non nul de chaque ligne non nulle (en partant de la gauche).
Un SL est échelonné par lignes lorsque :
- Si une ligne est nulle, toutes les lignes suivantes le sont aussi
- Á partir de la deuxième ligne, dans chaque ligne non nulle, le pivot est situé strictement à droite du pivot de la ligne précédente.
Dans un SL échelonné par lignes, on dit qu’une inconnue est principale si sur une des lignes du système, son coefficient est un pivot. Elle est dite secondaire (ou paramètre) sinon.
Un SL échelonné est compatible (au moins une solution) si et seulement s’il ne comporte pas de pivot sur la colonne des seconds membres.
Un SL échelonné compatible a une unique solution si et seulement s’il n’a que des inconnues principales.
Un SL triangulaire (ou la matrice associée) échelonné est réduit lorsque tous ses pivots sont égaux à 1 et chaque pivot est le seul coefficient non nul sur sa colonne.
Toute matrice est équivalente par lignes à une unique matrice échelonnée réduite.
Soit S un SL et A la matrice du SLH associé. Le rang de S est le nombre de pivots de la matrice réduite échelonnée équivalente par lignes à A.
Le rang d’un SL S s’obtient comme le nombre de pivots dans n’importe quel système échelonné équivalent à S. Dans l’écriture paramétrique des solutions de S, le nombre de paramètres est égal à la différence entre le nombre d’inconnues et le rang de S.
MATRICES
![]()
![]()
Matrices carrées – 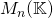
Soient ![]() et
et ![]() deux matrices carrées de
deux matrices carrées de ![]() telles que
telles que ![]()
![Rendered by QuickLaTeX.com \[ \forall k \in \mathbb{N}^* \qquad (A + B)^k = \sum_{p=0}^k \binom{k}{p} A^P B^{k-p} \qquad A^k - B^k = (A-B) \sum_{p=0}^{k-1} A^p B^{k-p-1} \]](http://www.rozenblum.com/wp-content/ql-cache/quicklatex.com-f8e32758d2d0a36c55c023cca32bf3a5_l3.png)
Une matrice scalaire est une matrice diagonale dont tous les coefficients sont égaux. Les matrices scalaires commutent avec toutes les autres.
A nilpotente : ![]() tel que
tel que ![]() .
.
Algorithme du pivot :
Matrices élémentaires dans ![]() :
:
- Matrice de transposition :
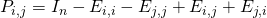
- Matrice de dilatation :
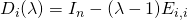
- Matrice de transvection :
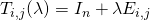
Soit ![]() :
:
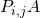 est la matrice obtenue en échangeant les lignes i et j de
est la matrice obtenue en échangeant les lignes i et j de 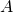 .
.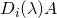 est la matrice obtenue en multipliant la ligne i de
est la matrice obtenue en multipliant la ligne i de 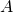 par
par 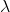 .
.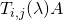 est la matrice obtenue en ajoutant à la ligne i de
est la matrice obtenue en ajoutant à la ligne i de 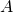 sa ligne j multipliée par
sa ligne j multipliée par 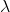 .
.
Pour toute matrice ![]() , il existe une matrice échelonnée réduite unique en ligne
, il existe une matrice échelonnée réduite unique en ligne ![]() et une matrice
et une matrice ![]() , produit de matrices élémentaires, telles que
, produit de matrices élémentaires, telles que ![]() . Même propriété pour les colonnes.
. Même propriété pour les colonnes.
Matrices inversibles – 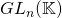
![]()
![]()
Une matrice diagonale est inversible si et seulement si ses coefficients sont tous non nuls. Son inverse est la matrice diagonale formée de l’inverse de tous ses coefficients.

