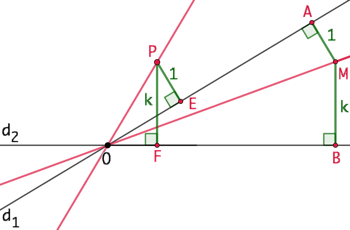
 Étant donnés deux droites
Étant donnés deux droites ![]() et
et ![]() sécantes en O et un nombre réel positif
sécantes en O et un nombre réel positif ![]() , le lieu géométrique des points dont les distances à ces deux droites sont dans un rapport constant
, le lieu géométrique des points dont les distances à ces deux droites sont dans un rapport constant ![]() , est constitué de la réunion de deux droites (OM) et (OP).
, est constitué de la réunion de deux droites (OM) et (OP).
on a ![]() .
.
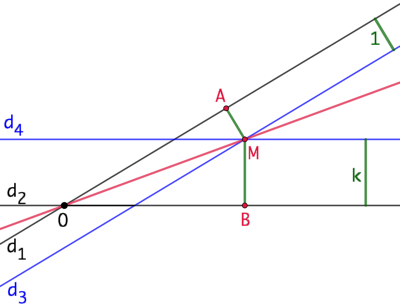 Construction :
Construction :
- On trace la droite
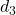 , parallèle de
, parallèle de 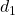 à une distance de 1 unité de
à une distance de 1 unité de 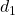 ;
; - On trace la droite
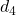 , parallèle de
, parallèle de 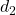 à une distance
à une distance 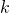 de
de 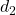 .
. - M, point d’intersection de
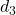 et
et 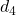 est par construction l’un des points recherchés.
est par construction l’un des points recherchés. - La droite (OM) est le lieu recherché.
L’autre droite (OP) s’obtient de manière similaire en traçant la droite symétrique de ![]() par rapport
par rapport ![]() .
.
Explications :
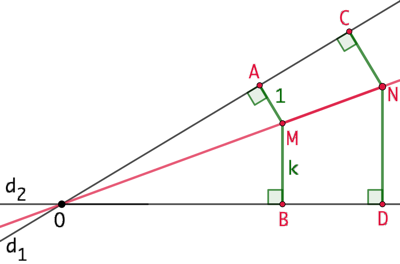 Soient N un point de la droite (OM), C et D les projections orthogonales respectives de N sur
Soient N un point de la droite (OM), C et D les projections orthogonales respectives de N sur ![]() et
et ![]() .
.
On va appliquer le théorème de Thales au triangles NCO et NDO :
![]() et
et ![]()
Donc : ![]() , soit
, soit ![]() .
.
La démonstration pour (OP) s’obtient de manière similaire. On vient donc de démontrer que tous les points de (ON) et de (OP) conviennent.
Sont-ils les seuls ?
Soient deux points distincts M et N tels que ![]() , ou ce qui est équivalent que
, ou ce qui est équivalent que ![]()
Soient O1 le point d’intersection de (MN) avec (OC), et O2 le point d’intersection de (MN) avec (OD). On va montrer que O1 et O2 sont confondus avec O.
Les triangles O1MA et O1NC sont semblables donc ![]() .
.
Les triangles O2MB et O2ND sont semblables donc ![]() .
.
Comme ![]() , il vient
, il vient ![]() .
.
Comme M et N sont distincts, les points O1 et O2 sont confondus avec O. Par conséquent, le point N appartient à la droite (OM).
![]() Remarque : Pourquoi les points O1 et O2 sont confondus si
Remarque : Pourquoi les points O1 et O2 sont confondus si ![]() .
.
![]() alors
alors ![]() .
.
Si on prend N comme origine du repère de la droite (NM), on obtient : ![]() .
.
Après développement et simplification, il vient : ![]() , ce qui achève de prouver que les points O1 et O2 sont confondus.
, ce qui achève de prouver que les points O1 et O2 sont confondus.
