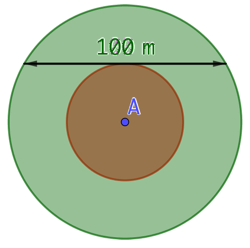
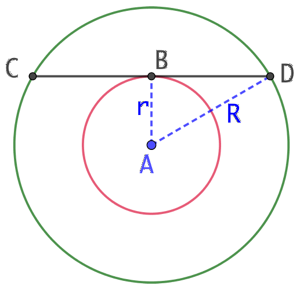
Une pelouse est délimitée par deux cercles concentriques de rayon r et R tels que CD = 100 m et la droite (CD) est tangente au petit cercle en B. On veut déterminer l’aire de la pelouse.
Explications :
et 
. 
est un angle droit puisque (CD) est tangente au cercle en B.
D’après le théorème de Pythagore : 
. Donc 
. On a aussi 
. Ce qui prouve que B est le milieu de [CD]. Donc BD = 50.
L’aire P de la pelouse est égale à l’aire du disque de rayon R moins l’aire du disque de rayon r. Donc 
.
